Measures of degeneracy and redundancy in biological networks
- PMID: 10077671
- PMCID: PMC15929
- DOI: 10.1073/pnas.96.6.3257
Measures of degeneracy and redundancy in biological networks
Abstract
Degeneracy, the ability of elements that are structurally different to perform the same function, is a prominent property of many biological systems ranging from genes to neural networks to evolution itself. Because structurally different elements may produce different outputs in different contexts, degeneracy should be distinguished from redundancy, which occurs when the same function is performed by identical elements. However, because of ambiguities in the distinction between structure and function and because of the lack of a theoretical treatment, these two notions often are conflated. By using information theoretical concepts, we develop here functional measures of the degeneracy and redundancy of a system with respect to a set of outputs. These measures help to distinguish the concept of degeneracy from that of redundancy and make it operationally useful. Through computer simulations of neural systems differing in connectivity, we show that degeneracy is low both for systems in which each element affects the output independently and for redundant systems in which many elements can affect the output in a similar way but do not have independent effects. By contrast, degeneracy is high for systems in which many different elements can affect the output in a similar way and at the same time can have independent effects. We demonstrate that networks that have been selected for degeneracy have high values of complexity, a measure of the average mutual information between the subsets of a system. These measures promise to be useful in characterizing and understanding the functional robustness and adaptability of biological networks.
Figures
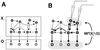
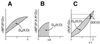
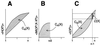


References
-
- Edelman G M. In: The Mindful Brain. Edelman G M, Mountcastle V B, editors. Cambridge, MA: MIT Press; 1978. pp. 51–100.
-
- Edelman G M. Neural Darwinism: The Theory of Neuronal Group Selection. New York: Basic Books; 1987. - PubMed
-
- Edelman G M, editor. Cellular Selection and Regulation in the Immune Response. New York: Raven; 1974. pp. 1–37.
-
- Kolb B, Whishaw I Q. Fundamentals of Human Neuropsychology. New York: Freeman; 1996.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

