Retinal waves are governed by collective network properties
- PMID: 10212317
- PMCID: PMC6782231
- DOI: 10.1523/JNEUROSCI.19-09-03580.1999
Retinal waves are governed by collective network properties
Abstract
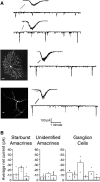
Propagating neural activity in the developing mammalian retina is required for the normal patterning of retinothalamic connections. This activity exhibits a complex spatiotemporal pattern of initiation, propagation, and termination. Here, we discuss the behavior of a model of the developing retina using a combination of simulation and analytic calculation. Our model produces spatially and temporally restricted waves without requiring inhibition, consistent with the early depolarizing action of neurotransmitters in the retina. We find that highly correlated, temporally regular, and spatially restricted activity occurs over a range of network parameters; this ensures that such spatiotemporal patterns can be produced robustly by immature neural networks in which synaptic transmission by individual neurons may be unreliable. Wider variation of these parameters, however, results in several different regimes of wave behavior. We also present evidence that wave properties are locally determined by a single variable, the fraction of recruitable (i.e., nonrefractory) cells within the dendritic field of a retinal neuron. From this perspective, a given local area's ability to support waves with a wide range of propagation velocities-as observed in experiment-reflects the variability in the local state of excitability of that area. This prediction is supported by whole-cell voltage-clamp recordings, which measure significant wave-to-wave variability in the amount of synaptic input a cell receives when it participates in a wave. This approach to describing the developing retina provides unique insight into how the organization of a neural circuit can lead to the generation of complex correlated activity patterns.
Figures




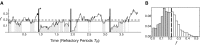
References
-
- Borges S, Gleason E, Frerking M, Wilson M. Neurotensin induces calcium oscillations in cultured neurons. Vis Neurosci. 1996;13:311–318. - PubMed
-
- Catsicas M, Bonness V, Becker D, Mobbs P. Spontaneous Ca2+ transients and their transmission in the developing chick retina. Curr Biol. 1998;8:283–286. - PubMed
-
- Copenhagen DR. Retinal development: on the crest of an exciting wave. Curr Biol. 1996;6:1368–1370. - PubMed
-
- Feller MB, Wellis DP, Stellwagen D, Werblin FS, Shatz CJ. Requirement for cholinergic synaptic transmission in the propagation of spontaneous retinal waves. Science. 1996;272:1182–1187. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
