Functional micro-organization of primary visual cortex: receptive field analysis of nearby neurons
- PMID: 10234033
- PMCID: PMC6782727
- DOI: 10.1523/JNEUROSCI.19-10-04046.1999
Functional micro-organization of primary visual cortex: receptive field analysis of nearby neurons
Abstract
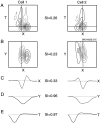
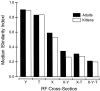
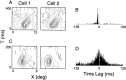
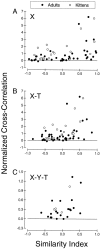
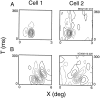
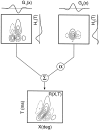
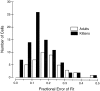
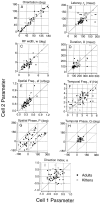
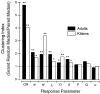
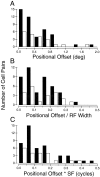
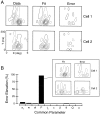
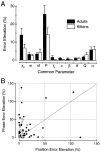
It is well established that multiple stimulus dimensions (e.g., orientation and spatial frequency) are mapped onto the surface of striate cortex. However, the detailed organization of neurons within a local region of striate cortex remains unclear. Within a vertical column, do all neurons have the same response selectivities? And if not, how do they most commonly differ and why? To address these questions, we recorded from nearby pairs of simple cells and made detailed spatiotemporal maps of their receptive fields. From these maps, we extracted and analyzed a variety of response metrics. Our results provide new insights into the local organization of striate cortex. First, we show that nearby neurons seldom have very similar receptive fields, when these fields are characterized in space and time. Thus, there may be less redundancy within a column than previously thought. Moreover, we show that correlated discharge increases with receptive field similarity; thus, the local dissimilarity between neurons may allow for noise reduction by response pooling. Second, we show that several response variables are clustered within striate cortex, including some that have not received much attention such as response latency and temporal frequency. We also demonstrate that other parameters are not clustered, including the spatial phase (or symmetry) of the receptive field. Third, we show that spatial phase is the single parameter that accounts for most of the difference between receptive fields of nearby neurons. We consider the implications of this local diversity of spatial phase for population coding and construction of higher-order receptive fields.
Figures




Similar articles
-
Receptive-field maps of correlated discharge between pairs of neurons in the cat's visual cortex.J Neurophysiol. 1994 Jan;71(1):330-46. doi: 10.1152/jn.1994.71.1.330. J Neurophysiol. 1994. PMID: 8158235
-
Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex. I. General characteristics and postnatal development.J Neurophysiol. 1993 Apr;69(4):1091-117. doi: 10.1152/jn.1993.69.4.1091. J Neurophysiol. 1993. PMID: 8492151
-
High-resolution two-dimensional spatial mapping of cat striate cortex using a 100-microelectrode array.Neuroscience. 2001;105(1):19-31. doi: 10.1016/s0306-4522(01)00174-9. Neuroscience. 2001. PMID: 11483297
-
The contribution of vertical and horizontal connections to the receptive field center and surround in V1.Neural Netw. 2004 Jun-Jul;17(5-6):681-93. doi: 10.1016/j.neunet.2004.05.002. Neural Netw. 2004. PMID: 15288892 Review.
-
Visual field maps in human cortex.Neuron. 2007 Oct 25;56(2):366-83. doi: 10.1016/j.neuron.2007.10.012. Neuron. 2007. PMID: 17964252 Review.
Cited by
-
Functional interactions among neurons within single columns of macaque V1.Elife. 2022 Nov 2;11:e79322. doi: 10.7554/eLife.79322. Elife. 2022. PMID: 36321687 Free PMC article.
-
Permanent functional reorganization of retinal circuits induced by early long-term visual deprivation.J Neurosci. 2009 Oct 28;29(43):13691-701. doi: 10.1523/JNEUROSCI.3854-09.2009. J Neurosci. 2009. PMID: 19864581 Free PMC article.
-
Interspike intervals, receptive fields, and information encoding in primary visual cortex.J Neurosci. 2000 Mar 1;20(5):1964-74. doi: 10.1523/JNEUROSCI.20-05-01964.2000. J Neurosci. 2000. PMID: 10684897 Free PMC article.
-
Analyzing variability in neural responses to complex natural sounds in the awake songbird.J Neurophysiol. 2009 Jun;101(6):3147-57. doi: 10.1152/jn.90917.2008. Epub 2009 Apr 8. J Neurophysiol. 2009. PMID: 19357333 Free PMC article.
-
Differential clustering of visual and choice- and saccade-related activity in macaque V3A and CIP.J Neurophysiol. 2024 Apr 1;131(4):709-722. doi: 10.1152/jn.00285.2023. Epub 2024 Mar 13. J Neurophysiol. 2024. PMID: 38478896 Free PMC article.
References
-
- Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. - PubMed
-
- Albrecht DG, Geisler WS. Motion selectivity and the contrast-response function of simple cells in the visual cortex. Vis Neurosci. 1991;7:531–546. - PubMed
-
- Berman NE, Wilkes ME, Payne BR. Organization of orientation and direction selectivity in areas 17 and 18 of cat cerebral cortex. J Neurophysiol. 1987;58:676–699. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
