Pearling in cells: a clue to understanding cell shape

Abstract

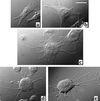
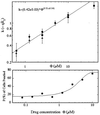
Gradual disruption of the actin cytoskeleton induces a series of structural shape changes in cells leading to a transformation of cylindrical cell extensions into a periodic chain of "pearls." Quantitative measurements of the pearling instability give a square-root behavior for the wavelength as a function of drug concentration. We present a theory that explains these observations in terms of the interplay between rigidity of the submembranous actin shell and tension that is induced by boundary conditions set by adhesion points. The theory allows estimation of the rigidity and thickness of this supporting shell. The same theoretical considerations explain the shape of nonadherent edges in the general case of untreated cells.

Figure 1

Microscope images taken in differential interference contrast (×63, oil-immersion objective) of SVT2 cells in varying degree of arborization after treatment with LatA. Concentrations Φ of the drug are (a) control Φ = 0; (b) Φ = 0.62 μM; (c) Φ = 1.25μM; (d) Φ = 2.5 μM; and (e) Φ = 10 μM. a and b are most probably mononuclear, whereas in c-e we chose more spherical, multinuclear cells. This illustrates the arborization by enhancing both the symmetry and the number of arbors. (Bar = 20 μm.)

Figure 2

Pearling in an SVT2 cell treated with 2.5 μM LatA and fixed in paraformaldehyde. All samples included in the statistical analysis were fixed and then viewed in a differential interference contrast microscope by using a computer-enhanced video system. Dynamical observations were conducted in a temperature-stabilized dish held at 37°C. (Bar = 10 μm.)

Figure 3

(Upper) Nondimensional wave number k = 2πR₀/λ of the pearled state as function of the LatA concentration Φ. Samples were scanned by eye to identify cells with pearled tubular protrusions, and still video pictures were transferred to the computer for analysis. The diameter of pearls 2R, distances between them λ, and the diameter of tube sections connecting pearls δ were measured. In many of the cells for which we identified pearling, the instability was in the nonlinear state with a periodic array of isolated pearls rather than a small-amplitude sinusoidal modulation. In such cases, the wavelength was taken as the distance between pearls. To determine the dimensionless wavenumber of the instability 2πR₀/λ, we needed to know R₀, the initial unperturbed tube radius, which was unknown for fixed cells. Hence, we used volume conservation along the tube: k = 2πR₀/λ = 2π(4R³/3λ³ + δ²/λ² − 2Rδ²/λ³)^1/2. For each drug concentration, we averaged up to 20 tubes and repeated the measurements at least once for almost all drug concentrations, with good reproducibility in each case. At low concentrations (Φ ≤ 0.5 μM) the wavelength measurements are noisy and therefore unreliable. At high concentrations, a trend to saturation of the wavenumber begins to be observed. Accordingly, we do not present the very low Φ points and did not consider them or the highest Φ point in fitting the power law. (Lower) Percentage of cells in which at least one cylinder has undergone pearling as a function of LatA concentration Φ. About 100 cells were counted per drug concentration. The line is a fit to an error function centered around Φ_c = 2.5 μM and with a width s = 3 μM. This is an integral of the Gaussian distribution erf(Φ) = C(2πs²)^−1/2∫_−∞^Φexp[(Φ′ − Φ_c)²/2s²]dΦ′. A fraction of about (1 − C) = 25% of the cells do not pearl even at high Φ.

Figure 4

Shapes of cells calculated from the theory as a function of the changing ratio between the balanced surface tension and effective elastic line tension at their edges. The calculation begins by placing a symmetric polygonal cell with n adhesion points lying on the unit circle (n = 3 for a–d and n = 7 for e–h). The parameter that determines the shape is then the radius R_∗ = γ/σ, measured in units of the distance between adhesion points. The values for a–d are R_∗ = 2.31, 1.15, 0.80, and 0.58 and for e–h are R_∗ = 1.15, 0.58, 0.40, and 0.23. a and e represent untreated cells, each with different symmetry, determined by the number of adhesion points. In a–d, we depict a more polar cell with three adhesion points, whereas in e–h, a more spherical cell like those in Fig. 1 c–e is produced. As the concentration of LatA Φ increases, the radius of curvature R_∗ that defines the arcs of cell membrane that hang between the adhesion points decreases (b and f). Eventually, when R_∗ is too small for the membrane to bridge the distance between adhesion points, the cell develops cylindrical protrusions (c and g). When the actin cortex rigidity of the collapsing cell is decreased below a critical value, these growing protrusions become unstable with respect to the pearling instability (d and h). Perspective and the cell height were added for illustration purposes, along with pearls on one cylinder in the final stages (d and h).