Continuous and lurching traveling pulses in neuronal networks with delay and spatially decaying connectivity

Abstract

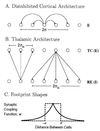
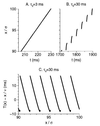
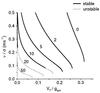
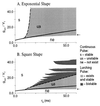
Propagation of discharges in cortical and thalamic systems, which is used as a probe for examining network circuitry, is studied by constructing a one-dimensional model of integrate-and-fire neurons that are coupled by excitatory synapses with delay. Each neuron fires only one spike. The velocity and stability of propagating continuous pulses are calculated analytically. Above a certain critical value of the constant delay, these pulses lose stability. Instead, lurching pulses propagate with discontinuous and periodic spatio-temporal characteristics. The parameter regime for which lurching occurs is strongly affected by the footprint (connectivity) shape; bistability may occur with a square footprint shape but not with an exponential footprint shape. For strong synaptic coupling, the velocity of both continuous and lurching pulses increases logarithmically with the synaptic coupling strength g(syn) for an exponential footprint shape, and it is bounded for a step footprint shape. We conclude that the differences in velocity and shape between the front of thalamic spindle waves in vitro and cortical paroxysmal discharges stem from their different effective delay; in thalamic networks, large effective delay between inhibitory neurons arises from their effective interaction via the excitatory cells which display postinhibitory rebound.

Figure 1

(A) Synaptic architecture of the cortical and thalamic models. Both have a one-dimensional architecture, with the coupling between cells decaying with their distance. The footprint lengths are denoted by σ (3, 20). In the case of two populations, the first and second letters in the subscript denote the pre- and postsynaptic populations respectively. (A) Disinhibited cortical model: a chain of excitatory (E) cells. (B) Thalamic model. Inhibitory (I) RE cells inhibit excitatory (E) TC cells, and TC cells excite RE cells. Mutual inhibition between RE cells is neglected because it has relatively small effect on discharge propagation (16, 19). (C) Exponential (solid line) and square (dashed line) footprint shapes.

Figure 2

(A and B) Rastergrams obtained from simulating Eqs. 2, 3, and 5 with the condition that each neuron can fire only one spike. Parameters: τ₀ = 30 ms, τ₂ = 2 ms, g_synV_T = 10, c → ∞, N = 5 × 10⁴, ρ = 500; for these parameters, τ_dc = 11.15 ms. The solid circles represent the firing time of neurons as a function of their normalized position x/σ; spikes of only one out of every 50 neuron are plotted. Together, the groups of solid circles looks almost like one continuous line. (A) For τ_d < τ_dc (3 ms), a continuous pulse is obtained. (B) For τ_d > τ_dc (30 ms), the pulse is lurching. (C) The fluctuation around the constant-velocity solutions, T(x) − x/ν are plotted as a function of position x/σ for the same parameters as in B, to demonstrate the oscillatory nature of the lurching pulse. The firing times of all the neurons are plotted here as solid dots.

Figure 3

The velocity of the continuous pulse as a function of V_T/g_syn for several values of τ_d and exponential footprint shape (Eq. 14). The wide lines represent stable pulses and the narrow lines represent unstable pulses. The number above each line, from 0 to 50, denotes the value of τ_d. Parameters: τ₀ = 30 ms, τ₂ = 2 ms.

Figure 4

Regimes of existence and stability of the continuous and lurching pulses in the τ_d-ν plane are shown in A for exponential footprint shape and in B for square footprint shape. Parameters are as in Fig 3. The boundaries of the regime in which the lurching pulse exists and is stable were computed from numerical simulations, in which a pulse was initiated by a “shock” initial stimulus; N = 20,000, ρ = 50. The solid line denotes the minimal possible velocity as a function of g_syn; the continuous pulse becomes unstable (via a Hopf bifurcation) on the dashed line. The continuous pulse is therefore stable above both the solid and long dashed line, as denoted by “s.” It is unstable between the two lines, as denoted by “us,” and does not exist below the continuous line, as denoted by “ne.” The light-gray shading represents the region for which lurching pulses (and not continuous pulses) are obtained. Bistable regimes, in which the continuous pulse can coexist with the lurching pulse, are denoted by the dark-gray shading. For the square footprint shape (B), but not for the exponential footprint shape, there is such a bistable regime that has a “tongue-like” structure. The arrow at the right of each graph represents the minimal values of g_syn for which the lurching pulse is found in simulations for τ_d → ∞.

Figure 5

The normalized length of the lurching period L/σ as a function of g_syn/V_T. The analytical solution for the case τ₁ = 0, τ₂ ≪ τ₀ ≪ τ_d (Eq. 18) is represented by the solid line. Simulations were carried out with N = 200,000 and ρ = 500. Simulations results with the corresponding parameter set: τ_d = 1000 ms, τ₀ = 30 ms, τ₁ = 0, τ₂ = 0.002 ms, denoted by ○, fit the analytical solutions almost exactly. The symbol × denotes simulations with τ_d = 20 ms, τ₀ = 30 ms, τ₁ = 0, τ₂ = 0.002 ms; the symbol ∗ denotes simulations with τ_d = 20 ms, τ₀ = 30 ms, τ₁ = 0, τ₂ = 2 ms; and the symbol □ denotes simulations with τ_d = 20 ms, τ₀ = 30 ms, τ₁ = 0.3, τ₂ = 2 ms.