Activity-driven synapse elimination leads paradoxically to domination by inactive neurons
- PMID: 10559405
- PMCID: PMC6782962
- DOI: 10.1523/JNEUROSCI.19-22-09975.1999
Activity-driven synapse elimination leads paradoxically to domination by inactive neurons
Abstract
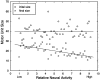
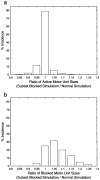
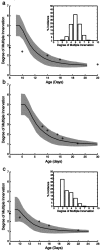
In early postnatal life, multiple motor axons converge at individual neuromuscular junctions. However, during the first few weeks after birth, a competitive mechanism eliminates all the inputs but one. This phenomenon, known as synapse elimination, is thought to result from competition based on interaxonal differences in patterns or levels of activity (for review, see Lichtman,1995). Surprisingly, experimental data support two opposite views of the role of activity: that active axons have a competitive advantage (Ribchester and Taxt, 1983; Ridge and Betz, 1984; Balice-Gordon and Lichtman, 1994) and that inactive axons have a competitive advantage (Callaway et al., 1987, 1989). To understand this paradox, we have formulated a mathematical model of activity-mediated synapse elimination. We assume that the total amount of transmitter released, rather than the frequency of release, mediates synaptic competition. We further assume that the total synaptic area that a neuron can support is metabolically constrained by its activity level and size. This model resolves the paradox by showing that a competitive advantage of higher frequency axons early in development is overcome at later stages by greater synaptic efficacy of axons firing at a lower rate. This model both provides results consistent with experiments in which activity has been manipulated and an explanation for the origin of the size principle (Henneman, 1985).
Figures
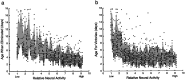
Similar articles
-
Terminal Schwann cell and vacant site mediated synapse elimination at developing neuromuscular junctions.Sci Rep. 2019 Dec 9;9(1):18594. doi: 10.1038/s41598-019-55017-w. Sci Rep. 2019. PMID: 31819113 Free PMC article.
-
Genetic evidence that relative synaptic efficacy biases the outcome of synaptic competition.Nature. 2003 Jul 24;424(6947):430-4. doi: 10.1038/nature01844. Nature. 2003. PMID: 12879071
-
Neuromuscular NMDA Receptors Modulate Developmental Synapse Elimination.J Neurosci. 2016 Aug 24;36(34):8783-9. doi: 10.1523/JNEUROSCI.1181-16.2016. J Neurosci. 2016. PMID: 27559162 Free PMC article.
-
Developmental neuromuscular synapse elimination: Activity-dependence and potential downstream effector mechanisms.Neurosci Lett. 2020 Jan 23;718:134724. doi: 10.1016/j.neulet.2019.134724. Epub 2019 Dec 23. Neurosci Lett. 2020. PMID: 31877335 Free PMC article. Review.
-
Activity-dependent synaptic competition at mammalian neuromuscular junctions.News Physiol Sci. 2004 Jun;19:85-91. doi: 10.1152/nips.01464.2003. News Physiol Sci. 2004. PMID: 15143199 Review.
Cited by
-
Losing the battle but winning the war: game theoretic analysis of the competition between motoneurons innervating a skeletal muscle.Front Comput Neurosci. 2012 Mar 30;6:16. doi: 10.3389/fncom.2012.00016. eCollection 2012. Front Comput Neurosci. 2012. PMID: 22479244 Free PMC article.
-
A neural algorithm for computing bipartite matchings.Proc Natl Acad Sci U S A. 2024 Sep 10;121(37):e2321032121. doi: 10.1073/pnas.2321032121. Epub 2024 Sep 3. Proc Natl Acad Sci U S A. 2024. PMID: 39226341 Free PMC article.
-
Structure and Function of the Mammalian Neuromuscular Junction.Compr Physiol. 2022 Aug 11;12(4):3731-3766. doi: 10.1002/cphy.c210022. Compr Physiol. 2022. PMID: 35950651 Free PMC article.
-
Competition is a driving force in topographic mapping.Proc Natl Acad Sci U S A. 2011 Nov 22;108(47):19060-5. doi: 10.1073/pnas.1102834108. Epub 2011 Nov 7. Proc Natl Acad Sci U S A. 2011. PMID: 22065784 Free PMC article.
-
Activity-dependent refinement of axonal projections forms one-to-one connection pattern in the developing chick ciliary ganglion.Front Cell Neurosci. 2025 Apr 9;19:1560402. doi: 10.3389/fncel.2025.1560402. eCollection 2025. Front Cell Neurosci. 2025. PMID: 40271539 Free PMC article.
References
-
- Balice-Gordon RJ, Lichtman JW. Long-term synapse loss induced by focal blockade of postsynaptic receptors. Nature. 1994;372:519–524. - PubMed
-
- Balice-Gordon RJ, Chua CK, Nelson CC, Lichtman JW. Gradual loss of synaptic cartels precedes axon withdrawal at developing neuromuscular junctions. Neuron. 1993;11:801–815. - PubMed
-
- Bennett MR, Robinson J. Growth and elimination of nerve terminals at synaptic sites during polyneuronal innervation of muscle cells: a trophic hypothesis. Proc R Soc Lond B Biol Sci. 1989;235:299–320. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
