Dissociation of HIV-1 from follicular dendritic cells during HAART: mathematical analysis

Abstract

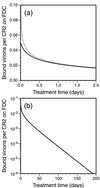
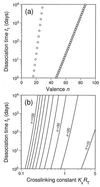
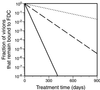
Follicular dendritic cells (FDC) provide a reservoir for HIV type 1 (HIV-1) that may reignite infection if highly active antiretroviral therapy (HAART) is withdrawn before virus on FDC is cleared. To estimate the treatment time required to eliminate HIV-1 on FDC, we develop deterministic and stochastic models for the reversible binding of HIV-1 to FDC via ligand-receptor interactions and examine the consequences of reducing the virus available for binding to FDC. Analysis of these models shows that the rate at which HIV-1 dissociates from FDC during HAART is biphasic, with an initial period of rapid decay followed by a period of slower exponential decay. The speed of the slower second stage of dissociation and the treatment time required to eradicate the FDC reservoir of HIV-1 are insensitive to the number of virions bound and their degree of attachment to FDC before treatment. In contrast, the expected time required for dissociation of an individual virion from FDC varies sensitively with the number of ligands attached to the virion that are available to interact with receptors on FDC. Although most virions may dissociate from FDC on the time scale of days to weeks, virions coupled to a higher-than-average number of ligands may persist on FDC for years. This result suggests that HAART may not be able to clear all HIV-1 trapped on FDC and that, even if clearance is possible, years of treatment will be required.

Figure 1

Reaction scheme. Complement opsonized virus is held on FDC through interactions between CR2 and terminal C3 fragments on HIV-1.

Figure 2

Dissociation of HIV-1 from FDC during HAART. The number of bound virions per CR2 on FDC, Σ_i=1ⁿ B_i/R_T, is plotted as a function of time t. Treatment begins at t = 0. For t > 0, we assume there is no attachment of HIV-1 to FDC. The time course of dissociation during (a) the first 2 d of treatment or (b) the first 200 d of treatment is determined from Eqs. 1 and 2 with n = 20, K_xR_T = 1.1427 and k_r = k_−x = 0.1 s⁻¹. After the value of n is specified, the value of K_xR_T is chosen so that the level of virus on FDC after 180 d of treatment is 10,000-fold less than that after 2 d of treatment. The dotted line in a is based on the initial condition B₁ = R_T (each receptor is initially bound to a single virion). The solid line is based on a more realistic initial condition, which is determined from the steady-state form of Eqs. 1 and 2 with the associative rate αVR (αV = 3.5576 × 10⁻⁶ s⁻¹) added to the expression for dB₁/dt in Eq. 1. With this initial condition, Σ_i=1ⁿ B_i/R_T = 0.05, and virions are distributed in various bound states at t = 0.

Figure 3

Influence of (a) valence n and (b) dimensionless crosslinking constant K_xR_T on the expected dissociation time of an individual virion, t₁. In a, t₁ is plotted as a function of n for K_xR_T = 1.1427 (circles) and K_xR_T = 0.2826 (squares) (cf. Table 1). In b, t₁ is plotted as a function of K_xR_T for n = 10, … , 100. Dissociation times are determined from Eq. 4 with k_r = 0.1 s⁻¹.

Figure 4

Fraction of virions initially on FDC that remain on FDC after treatment time t. The quantity Σ_jⁿ₌₁ P_1j, determined from Eq. 5, is plotted as a function of t for three cases: n = 60 (solid line), n = 65 (broken line), and n = 70 (dotted line). In all cases, k_r = k_−x = 0.1 s⁻¹ and K_xR_T = 0.2826 (cf. Table 1).