Human arm movements described by a low-dimensional superposition of principal components

Abstract

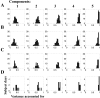
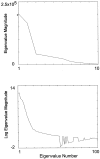
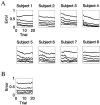
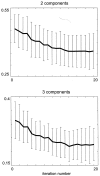
A new method for analyzing kinematic patterns during smooth movements is proposed. Subjects are asked to move the end of a two-joint manipulandum to copy a smooth initial target path. On subsequent trials the target path is the subject's actual movement from the preceding trial. Using Principal Components Analysis, it is shown that the trajectories have very low dimension and that they converge toward a linear superposition of the first few principal components. We show similar results for handwriting on an electronic pen tablet. We hypothesize that the low dimensionality and convergence are attributable to combined properties of the internal controller and the musculoskeletal system. The low dimensionality may allow for efficient descriptions of a large class of arm movements.

Fig. 1.

Example of iterated practice and the calculated principal components. A, Each row of the figure shows the recorded hand movements for a block of 20 trials. Each block was started with a new random target shape presented during the first two trials. Errors on the first trial are often the result of accommodation to a new shape. B, The shape of the first five eigenvectors (principal components) computed over 2400 movement trials. The first row shows the path in x–y coordinates, and the second and third rows show the x and y components as a function of time.C, Log–log plots of the instantaneous velocity versus curvature of the components, with numeric values of the average slope of the plot.

Fig. 2.

Histograms of movement approximation variance using from one to five principal components for all subjects. Eachpoint in the histograms represents 1 d for one subject. The horizontal axis shows the fraction of the total movement variance accounted for. A, Approximation for two dimensions of hand movement. B, Approximation for all subjects using the components from subject 1. The similarity of components between different subjects makes the approximation possible, but slightly worse than in A. C, Approximation for two dimensions of hand movement combined with three dimensions of unconstrained elbow movements for all subjects. The number of components remains low despite 250 dimensions in the input data. D, Approximation for pen tip position on an electronic drawing tablet. The same phenomenon holds, although in general each subject uses different components than in the manipulandum task.

Fig. 3.

Magnitude of the eigenvalues versus eigenvalue number for a single subject on 1 d (1200 movements). The same data is plotted for the first 10 components on a linear scale and for all 100 components on a log scale.

Fig. 4.

Approximation of trajectories within a single trial block using from one to five components. The top rowshows a single iterated block of 20 trials. Components are calculated from the movements of the entire day, and the second throughsixth rows show approximation of the movement trajectories using progressively fewer components. Note that the similarity between the actual movement and the approximations increases as the iteration continues.

Fig. 5.

Change in approximation error with iterated practice for each subject. A, From top tobottom in each figure, the lines indicate the decrease in error with from one to five components, showing that the first few components account for progressively increasing percentages of the total movement variance. The top line shows the decrease in error with approximation using one component, thesecond line shows the decrease for two components, and so on. The error is shown normalized to the total movement variance. Each plot is averaged over 20 movement blocks. Note that, for subject 1, the first two components combined account for an increasing percentage of the total variance, although the first component percentage decreases.B, Lack of convergence when the same target is presented at each trial (Subject 2). This shows that convergence is not simply an effect of repeated practice.

Fig. 6.

Average across subjects of the decrease in approximation error with increasing iteration, using two and three components. Error is averaged over blocks of 400 trials for eight subjects on multiple days. Error bars indicate 1 SD of the between-subject variation for a single iteration number.

Fig. 7.

Average sum squared distance from the final movement in a block, by iteration number. Distance is averaged over blocks of 400 trials for 8 subjects on multiple days. Error bars indicate 1 SD of the between-subject variation for a single iteration number. Note that the curve shows steady slow progression toward the final movement, but it does not show evidence of stabilizing near the final curve.

Fig. 8.

Example of iterated practice for simulation of an equilibrium-point controlled two-joint planar mechanical arm, shown as in Figure 1. Each row of the figure shows the simulated hand movements for a block of 20 trials.

Fig. 9.

Change in approximation error with iterated practice for simulation of equilibrium-point controlled two-joint planar mechanical arm, plotted as in Figure 5. From top tobottom in each figure, the lines indicate the decrease in error with from one to five components, averaged over 20 movement blocks.