Image registration using a symmetric prior--in three dimensions

Abstract

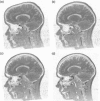
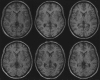
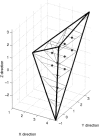
This paper describes a Bayesian method for three-dimensional registration of brain images. A finite element approach is used to obtain a maximum a posteriori estimate of the deformation field at every voxel of a template volume. The priors used by the MAP estimate penalize unlikely deformations and enforce a continuous one-to-one mapping. The deformations are assumed to have some form of symmetry, in that priors describing the probability distribution of the deformations should be identical to those for the inverses (i.e., warping brain A to brain B should not be different probablistically from warping B to A). A gradient descent algorithm is presented for estimating the optimum deformations.

Figure 1

The volume of the template image is divided into a mesh of irregular tetrahedra, where the vertexes of the tetrahedra are centered on the voxels. Groups of eight voxels are considered as little cubes. The volume of each cube is divided into five tetrahedra, in one of the two possible arrangements shown here. A face of a cube that is divided according to one arrangement, opposes with the face of a cube that has been divided the other way. Because of this, it is necessary to arrange the two conformations in a three‐dimensional checkerboard pattern.

Figure 2

A comparison of the different cost functions. The dotted line shows the potential estimated from (log(s _ii ))², where s _ii is the ith singular value of a Jacobian matrix. The solid line shows the new potential, which is based on (s ${}_{\text{2}}^{\text{ii}}$ + s ${}_{\text{−2}}^{\text{ii}}$ − 2)/4. For singular values very close to one, the potentials are almost identical.

Figure 3

A sagittal plane from two images registered together. The template (reference) image is shown in (d). (a) shows the source image after affine registration to the template image. The source image after the basis function registration is shown in (b), and the final registration result is in (c). The deformation fields are shown in Figure 4.

Figure 4

The deformation fields corresponding to the images in Figure 3. Two components (vertical and horizontal translations) of the field following affine and basis function registration are shown on the left, whereas the final deformation field is shown on the right.

Figure 5

A deformation computed by warping the first image to the second (left), and by taking the inverse of the deformation computed by warping the second to the first (right).

Figure 6

Images of six subjects registered using a 12‐parameter affine registration (see also Figs. 7 and 8). The affine registration matches the positions and sizes of the images.

Figure 7

Six subjects brains registered with both affine and basis function registration (see also Figs. 6 and 8). The basis function registration estimates the global shapes of the brains, but is not able to account for high spatial frequency warps.

Figure 8

The images of the six brains following affine and basis function registration, followed by high‐dimensional image registration using the methods described in this paper (see also Figs. 6 and 7). The high‐dimensional transformations are able to model high frequency deformations that cannot be achieved using the basis function approach alone.

Figure 9

Rendered surfaces of the original six brains. The white markers correspond to equivalent locations on the brain surfaces as estimated by the registration algorithm.

Figure 10

By combining the warps, it is possible to compute a mapping between any pair of images. In this example, the remaining images were all transformed to match the one shown at the lower left.

Figure 11

An illustration of how voxels are located within a tetrahedron.