Robust perfect adaptation in bacterial chemotaxis through integral feedback control

Abstract

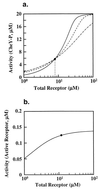
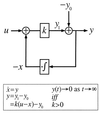
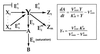
Integral feedback control is a basic engineering strategy for ensuring that the output of a system robustly tracks its desired value independent of noise or variations in system parameters. In biological systems, it is common for the response to an extracellular stimulus to return to its prestimulus value even in the continued presence of the signal-a process termed adaptation or desensitization. Barkai, Alon, Surette, and Leibler have provided both theoretical and experimental evidence that the precision of adaptation in bacterial chemotaxis is robust to dramatic changes in the levels and kinetic rate constants of the constituent proteins in this signaling network [Alon, U., Surette, M. G., Barkai, N. & Leibler, S. (1998) Nature (London) 397, 168-171]. Here we propose that the robustness of perfect adaptation is the result of this system possessing the property of integral feedback control. Using techniques from control and dynamical systems theory, we demonstrate that integral control is structurally inherent in the Barkai-Leibler model and identify and characterize the key assumptions of the model. Most importantly, we argue that integral control in some form is necessary for a robust implementation of perfect adaptation. More generally, integral control may underlie the robustness of many homeostatic mechanisms.

Figure 1

Robust and nonrobust perfect adaptation. The dependence of steady-state system activity on total receptor concentration was calculated by using equilibrium analysis for three concentrations of chemoattractant: (i) L = 0 (solid), (ii) L = 1 μM (dashed), and (iii) L = 1 mM (dashed–dot). The filled circle indicates the value of total receptor used in the model. (a) Spiro model. The system activity is measured in terms of the concentration of CheY-P. The intersection of the three lines, which coincides with the filled circle, represents the value of total receptor at which perfect adaptation exists. (b) Barkai–Leibler model. The system activity is measured in terms of the concentration of active receptor complexes. The three lines completely overlap. These plots were performed by using the program xppaut (34, 35).

Figure 2

A block diagram of integral feedback control. The variable u is the input for a process with gain k. The difference between the actual output y₁ and the steady-state output y₀ represents the normalized output or error, y. Integral control arises through the feedback loop in which the time integral of y, x, is fed back into the system. As a result, we have ẋ = y and y = 0 at steady-state for all u. In the Barkai–Leibler model of the bacterial chemotaxis signaling system, the chemoattractant is the input, receptor activity is the output, and −x approximates the methylation level of the receptors.

Figure 3

Robust regulation of the steady-state level of a pathway component. In this hypothetical biochemical pathway, the level of the component Y is maintained at a constant steady-state level by an integral feedback loop mediated by the regulator molecule A and the enzymes that produce and remove A, E₃ and E₄. Both the upstream molecules (X_i) and enzymes (E₁ⁱ) and the downstream molecules (Z_i) and enzymes (E₂ⁱ) do not influence the steady-state concentration of Y, Y₀, assuming that the system is stable. The equation for Y₀ was derived by using Michaelis–Menten kinetics and the assumption that E₄ is operating at saturation. V_max³ and V_max⁴ are the maximal velocities, and K_m³ and K_m⁴ are the Michaelis constants for E₃ and E₄.