A thixotropic effect in contracting rabbit psoas muscle: prior movement reduces the initial tension response to stretch
- PMID: 10835052
- PMCID: PMC2269955
- DOI: 10.1111/j.1469-7793.2000.00531.x
A thixotropic effect in contracting rabbit psoas muscle: prior movement reduces the initial tension response to stretch
Abstract
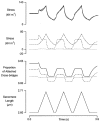
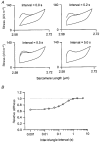
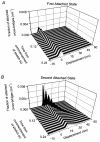
Paired ramp stretches and releases ('triangular length changes', typically 0.04 +/- 0.09L0 s-1; mean +/- s.e.m.) were imposed on permeabilised rabbit psoas fibre segments under sarcomere length control. In actively contracting fibres, the tension response to stretch was biphasic; tension rose more rapidly during the first 0. 005L0 of the imposed stretch than thereafter. Tension also dropped in a biphasic manner during shortening, and at the end of the length change was reduced below the steady state. If a second triangular length change was imposed shortly after the first, tension rose less sharply during the initial phase of lengthening, i.e. the stiffness of the muscle during the initial phase of the response was reduced in the second stretch. This is a thixotropic effect. If a third triangular length change was imposed on the muscle, the response was the same as that to the second. The time required to recover the original tension response was measured by varying the interval between triangular length changes. Recovery to steady state occurred at a rate of approximately 1 s-1. The stiffness of the muscle during the initial phase of the response scaled with the developed tension in pCa (= -log10[Ca2+]) solutions ranging from 6.3 (minimal activation) to 4.5 (saturating effect). The relative thixotropic reduction in stiffness measured using paired length changes was independent of the pCa of the activating solution. The thixotropic behaviour of contracting skeletal muscle can be explained by a cross-bridge model of muscle contraction in which the number of attached cross-bridges is temporarily reduced following an imposed movement.
Figures




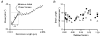
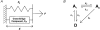
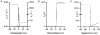
References
-
- Bartoo ML, Linke WA, Pollack GH. Basis of passive tension and stiffness in isolated rabbit myofibrils. American Journal of Physiology. 1997;273:C266–276. - PubMed
-
- Buchthal F, Kaiser E. The rheology of the cross striated muscle fibre with particular reference to isotonic conditions. Det Kongelige Danske Videnskabernes Selskab Biologiske Meddelser, Copenhagen. 1951;21:1–307.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

