Parking strategies for genome sequencing

Abstract

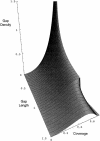
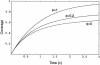
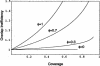
The parking strategy is an iterative approach to DNA sequencing. Each iteration consists of sequencing a novel portion of target DNA that does not overlap any previously sequenced region. Subject to the constraint of no overlap, each new region is chosen randomly. A parking strategy is often ideal in the early stages of a project for rapidly generating unique data. As a project progresses, parking becomes progressively more expensive and eventually prohibitive. We present a mathematical model with a generalization to allow for overlaps. This model predicts multiple parameters, including progress, costs, and the distribution of gap sizes left by a parking strategy. The highly fragmented nature of the gaps left after an initial parking strategy may make it difficult to finish a project efficiently. Therefore, in addition to our parking model, we model gap closing by walking. Our gap-closing model is generalizable to many other strategies. Our discussion includes modified parking strategies and hybrids with other strategies. A hybrid parking strategy has been employed for portions of the Human Genome Project.

Figure 1

Cartoon of the parking strategy. Cars arrive sequentially at an infinite curb and choose parking spots uniformly from all possible spots, subject to the constraint that they do not overlap any already-parked car. In the portion of the infinite curb illustrated here, only one additional car will fit. The left end of this car can be sited only within the darkened interval.

Figure 2

Gap length distribution. Gap density is the average number of left endpoints of gaps of a particular length that will be found in a unit interval of the infinite line at a particular time. The upper limit of coverage is the jamming limit, Rényi's number. The graph is arbitrarily truncated at a gap length of 1.5. For any fixed time, a cusp exists in the curve for gap density at a gap length equal to unity. At the jamming limit, all gaps are less than the length of a clone (L = 1; φ = 0).

Figure 3

Coverage versus time. Coverage is asymptotic to the jamming limit, which varies with the allowed overlap φ.

Figure 4

Cartoon of overlap parking. The central exclusion zone of a clone of length (1 − φ)L, shaded gray in the figure, may not overlap any other exclusion zone. Clones a and b overlap to the maximum possible extent, φL. The gap between clones b and c is the smallest gap that still allows for an additional clone to fit. However, the probability of a clone randomly being placed in this gap in any finite interval of time is zero. A single clone can fit with room to spare between clones c and d.

Figure 5

Jamming limit versus allowed overlap, φ. The jamming limit is unity for all allowed overlaps greater than or equal to one-half. The gray points are the averages of ten simulations of parking 150 kb clones on a 3Gb target.

Figure 6

Overlap inefficiency of parking. Overlap inefficiency is the ratio of the sum of the lengths of the clones sequenced to the length of unique target sequence produced. There is no such inefficiency for strict parking with no allowed overlap (φ = 0). Overlap inefficiency and coverage are parametrically related as functions of time ν; the resulting curves do not extend beyond their respective jamming limits. The curve for φ = 1 corresponds to the Clarke-Carbon equation.

Figure 7

Parking costs as a function of coverage. For small to moderate values of coverage, parking costs are roughly proportional to coverage, demonstrating that the cost burdens of screening and of overlap inefficiency are initially quite small. Near the jamming limit, these costs rise sharply as the number of screening operations to identify an appropriate clone for sequencing rises sharply. Dropping the cost of screening by almost two orders of magnitude provides only a marginal benefit shortly before the jamming limit. Allowing modest overlaps permits progress toward higher jamming limits at little cost increase. The curve for φ = 0 and r = 14 intersects the curve for φ = 0.2 and r = 1000 at 0.4493 coverage. In practice, the curve for φ = 1 and r = 14 would run at a slightly lower cost, as no screening would actually be done (any screening results would be ignored). For screening by partial sequencing, this cost savings would be small, as it would apply only to clones not fully sequenced. If this factor is taken into account, the curve for φ = 0 and r = 1000 also must be slightly adjusted. We left the curves unadjusted to facilitate comparison of the parameterization of the underlying equations.

Figure 8

Excess overlap versus gap length (constant clone length).

Figure 9

Expected excess overlap versus gap length (variable clone length). The model from the text is implemented such that the length for each walking step is drawn from a gamma distribution with mean 100 kb and standard deviation 14.4 kb. Each gray point represents the average of 10,000 simulations of this process; the simulations are consistent with the model. The damped oscillations decay towards an asymptote near 51 kb, just over half the average length of a clone.