Three-dimensional mapping of cortical thickness using Laplace's equation

Abstract

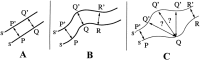
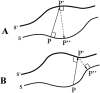
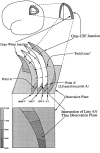
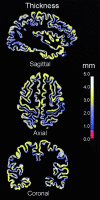
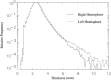
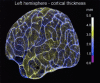
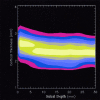
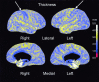
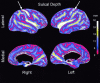
We present a novel, computerized method of examining cerebral cortical thickness. The normal cortex varies in thickness from 2 to 4 mm, reflecting the morphology of neuronal sublayers. Cortical pathologies often manifest abnormal variations in thickness, with examples of Alzheimer's disease and cortical dysplasia as thin and thick cortex, respectively. Radiologically, images are 2-D slices through a highly convoluted 3-D object. Depending on the relative orientation of the slices with respect to the object, it is impossible to deduce abnormal cortical thickness without additional information from neighboring slices. We approach the problem by applying Laplace's Equation (V2psi = 0) from mathematical physics. The volume of the cortex is represented as the domain for the solution of the differential equation, with separate boundary conditions at the gray-white junction and the gray-CSF junction. Normalized gradients of psi form a vector field, representing tangent vectors along field lines connecting both boundaries. We define the cortical thickness at any point in the cortex to be the pathlength along such lines. Key advantages of this method are that it is fully three-dimensional, and the thickness is uniquely defined for any point in the cortex. We present graphical results that map cortical thickness everywhere in a normal brain. Results show global variations in cortical thickness consistent with known neuroanatomy. The application of this technique to visualization of cortical thickness in brains with known pathology has broad clinical implications.

Figure 1

Example of a raw axial T1 MRI image with superimposed segmentation of cortex. Although the cortex indicated at point A appears thicker than that indicated at point B, subsequent analysis reveals their thickness to be almost identical. The discrepancy is an artifact of the three dimensional angle of intersection between the axial slice and the cortical surface.

Figure 2

Three two‐dimensional examples of thickness in different geometries. Panel A shows the thickness between two boundaries of parallel straight lines as orthogonal projections (e.g., lines P–P′ and Q–Q′ are perpendicular to both S and S′). Panel B also uses orthogonal projections but the boundaries are curvilinear with the distance between them much smaller than their radius of curvature. Panel C has two boundaries where the distance between them in not much smaller than their radius of curvature. The thickness based on orthogonal projections is compatible with example pathlengths P–P′, and R–R′, but not at pathlengths originating from point Q.

Figure 3

Two candidate definitions for thickness in a two‐dimensional example based on one orthogonal intersection. Panel A assumes an orthogonal projection from S which crosses to intersect S′, as exemplified by P–P′. Not the lack of reciprocity as the orthogonal projection from P′ does not return to P′. Panel B assumes a projection from S that crosses to orthogonally intersect S′. This is equivalent to finding the point P′ on S′ closest to a given point P lying on S. Again, there is a lack of reciprocity.

Figure 4

Two‐dimensional example of Laplace's method. Laplace's equation is solved between S and S′, which have predetermined boundary conditions of 10,000 V and 0 V, respectively. Three examples of resulting intermediate equipotential surfaces are indicated for 2,500 V, and 5,000 V, and 7,500 V. Field lines connecting S to S′ are defined as being everywhere orthogonal to all equipotential surfaces, as exemplified by the line connecting P to P′.

Figure 5

Three‐dimensional cartoon example of Laplace's method. The top panel shows a portion of cortex to be highlighted below. The middle panel converts that segment of cortex into a mathematical volume for Laplace's method. The gray‐CSF surface and gray‐white surfaces are fixed to boundary conditions of 0 V and 10,000 V, respectively, and Laplace's equation is solved in between. Two examples of resulting intermediate equipotential surfaces are indicated for 2,500 V and 7,500 V. Five example field lines are indicated connecting the two surfaces, which are everywhere orthogonal to all intermediate equipotential surfaces. The cortical thickness is defined anywhere in the cortical volume as the thickness of the field line passing through that point and connecting the two surfaces. The cortical volume intersects an “observation plane,” on which thickness results are mapped for tomographic visualization as exemplified in the bottom panel. For example, the line A–A′, with a pathlength of 2.8 mm, happens to intersect the observation plane. That region of the observation plane is then color‐coded for 2.8 mm with respect to the color bar.

Figure 6

Two‐dimensional cartoon showing the application of Laplace's method to an extracortical volume. The top panel schematically shows one hemisphere with one large sulcus, labeled by points A through P spaced equidistant along the cortical surface. The thickness of the cortex is coded by shades of gray, for example, the dark shade at D reflects increased thickness. Laplace's method is applied to the extracortical volume defined between the cortical surface and a smoothed extracortical surface. Field lines from Laplace's method connect the two surfaces (e.g., lines A–A′, through P–P′). Note the points A′ through P′ are no longer equidistant. The middle panel uses the field lines to translate the coded cortical thickness from the cortical surface to the extracortical surface. Thus, the thicker cortex at point D is mapped as a correspondingly darker shade at point D′. The bottom panel results from warping the points from the middle panel so they are now equidistant. The darker shade mapped at point D′ is now easily visualized.

Figure 7

Close‐up example of gradients of Laplace's solution in an axial plane from real data. The blue line represents the gray‐white junction, and the red line represents the gray‐CSF junction. The small arrows are projections of the gradient vectors in the axial plane. These arrows are tangent to the streamlines connecting the two surfaces. Arrows appear short when they are projecting predominantly out of the axial plane [e.g., at position (15,5)]. The gradients are insensitive to small segmentation errors as seen but the sulcal discontinuity at position (30,29).

Figure 8

Close‐up of three‐dimensional example of cortical volume from real data. The volume of data is roughly 10 × 10 × 10 voxels. The red surface is the gray‐white surface from a sulcal bank on the lateral aspect of one hemisphere. The three continuous curvilinear lines are intersections of three axial planes with the gray‐CSF surface, and thus lie on the gray‐CSF surface. The connecting lines are examples of streamlines using the Laplace method. The cortical thickness at any point in the cortical volume is defined as the length of the streamline passing through it and connecting the two surfaces.

Figure 9

Tomographic mapping of cortex to cortical thickness. The cortical volume is color‐coded for thickness such that red, blue, green, and yellow regions are 1, 2, 3, and 4 mm thick, respectively. The images are from the three cardinal planes of the left hemisphere from one scan.

Figure 10

Logarithmic histogram of frequency of cortical thickness from all calculated pathlengths, segregated by hemisphere. The most prevalent thickness in each hemisphere is about 2.5 mm. The falloff for both thinner and thicker cortex is nearly exponential. Significant differences between the hemispheres are not discernable. Thickness much larger than 7 mm are likely due to segmentation errors.

Figure 11

Lateral view of superficial surface of left hemisphere with a color‐coded mapping for cortical thickness. The color bar indicates any red, blue, green, and yellow cortex as being 1 mm, 2 mm, 3 mm, and 4 mm thick, respectively. The view is a direct projection of the externally visible and unwarped cortical surface, therefore, all mappings associated with sulcal cortex are not visualized. The high density of voxels lying on the sulcal banks visualizes the sulci. The defects at the anterior aspect of the temporal lobe are due to segmentation errors arising from the orbits.

Figure 12

A color‐coded contour plot shows the relationship between cortical thickness and sulcal depth. At each sulcal depth, a histogram of all cortical thickness is obtained. Each histogram is normalized to unity. The histograms are then “stacked” together to form a mathematical matrix that can be visualized as a two‐dimensional contour plot. There are seven contours at levels between 0.9 and 0.3. Bright colors (white‐yellow) at the highest contours reveal the most common cortical thickness at each sulcal depth. The downward trend of all contours from 2.63 mm in the superficial cortex to 2.30 mm in the interior cortex is interpreted as a 14% reduction in cortical thickness with cortical depth. The transition is mostly complete for cortex deeper than 6 mm.

Figure 13

Color‐coded mapping of cortical surface with cortical thickness. The cortex has been warped to improve visualization by flattening the sulcal geometry to an smoothed extracortical form while approximately conserving relative cortical surface areas. The color bar codes for cortical thickness such that red is 1 mm thick and yellow is 4 mm thick. This highlights the relative thinness of the posterior bank of the central sulcal that is seen as a dark band emanating from the superior aspect of both lateral projections. The four views are from one scan which represent medial and lateral views of the left and right hemisphere.

Figure 14

Color‐coded mapping of cortical surface with sulcal depth. The cortex has been warped to improve visualization by flattening the sulcal geometry to an smoothed extracortical form while approximately conserving relative cortical surface areas. The color bar codes for sulcal depth relative to the superficial cortical surface such that any non‐red color represents cortex lying within sulci. White dots are superimposed over any region of cortex that is thinner than 1.2 sigma of the mean thickness. This highlights the association between sulcal cortex with thinner cortex. The four views are from one scan which represent medial and lateral views of the left and right hemisphere.