The Flory isolated-pair hypothesis is not valid for polypeptide chains: implications for protein folding
- PMID: 11070081
- PMCID: PMC18804
- DOI: 10.1073/pnas.97.23.12565
The Flory isolated-pair hypothesis is not valid for polypeptide chains: implications for protein folding
Abstract
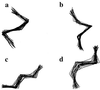
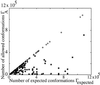
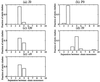
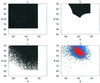
Using an all-atom representation, we exhaustively enumerate all sterically allowed conformations for short polyalanyl chains. Only intrachain interactions are considered, including one adjustable parameter, a favorable backbone energy (e.g., a peptide hydrogen bond). The counting is used to reevaluate Flory's isolated-pair hypothesis, the simplifying assumption that each phi,psi pair is sterically independent. This hypothesis is a conceptual linchpin in helix-coil theories and protein folding. Contrary to the hypothesis, we find that systematic local steric effects can extend beyond nearest-chain neighbors and can restrict the size of accessible conformational space significantly. As a result, the entropy price that must be paid to adopt any specific conformation is far less than previously thought.
Figures

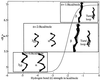
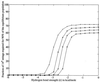
Comment in
-
Are denatured proteins ever random coils?Proc Natl Acad Sci U S A. 2000 Nov 7;97(23):12391-2. doi: 10.1073/pnas.97.23.12391. Proc Natl Acad Sci U S A. 2000. PMID: 11070072 Free PMC article. Review. No abstract available.
References
-
- Fowler R H, Guggenheim E A. Statistical Thermodynamics. London: Cambridge Univ. Press; 1939. p. 6.
-
- Levinthal C. In: How to Fold Graciously. Debrunner P, Tsibris J C M, Münck E, editors. Urbana, IL: Univ. of Illinois Press; 1969. pp. 22–24.
-
- Flory P J. Statistical Mechanics of Chain Molecules. New York: Wiley; 1969. p. 252.
-
- Zimm B H, Bragg J K. J Chem Phys. 1959;31:526–535.
-
- Lifson S, Roig A. J Chem Phys. 1961;34:1963–1974.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

