Learning of visuomotor transformations for vectorial planning of reaching trajectories
- PMID: 11102502
- PMCID: PMC6773094
- DOI: 10.1523/JNEUROSCI.20-23-08916.2000
Learning of visuomotor transformations for vectorial planning of reaching trajectories
Abstract
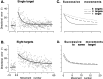
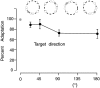
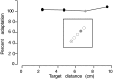
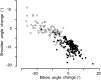
The planning of visually guided reaches is accomplished by independent specification of extent and direction. We investigated whether this separation of extent and direction planning for well practiced movements could be explained by differences in the adaptation to extent and directional errors during motor learning. We compared the time course and generalization of adaptation with two types of screen cursor transformation that altered the relationship between hand space and screen space. The first was a gain change that induced extent errors and required subjects to learn a new scaling factor. The second was a screen cursor rotation that induced directional errors and required subjects to learn new reference axes. Subjects learned a new scaling factor at the same rate when training with one or multiple target distances, whereas learning new reference axes took longer and was less complete when training with multiple compared with one target direction. After training to a single target, subjects were able to transfer learning of a new scaling factor to previously unvisited distances and directions. In contrast, generalization of rotation adaptation was incomplete; there was transfer across distances and arm configurations but not across directions. Learning a rotated reference frame only occurred after multiple target directions were sampled during training. These results suggest the separate processing of extent and directional errors by the brain and support the idea that reaching movements are planned as a hand-centered vector whose extent and direction are established via learning a scaling factor and reference axes.
Figures





References
-
- Bedford F. Perceptual and cognitive spatial learning. J Exp Psychol Hum Percept Perform. 1993;49:517–530. - PubMed
-
- Bock O. Adaptation of aimed arm movements to sensorimotor discordance: evidence for direction-independent gain control. Behav Brain Res. 1992;51:41–50. - PubMed
-
- Bock O. Scaling of joint torque during planar arm movements. Exp Brain Res. 1994;101:346–352. - PubMed
-
- Bock O, Burghoff M. Visuo-motor adaptation: evidence for a distributed amplitude control system. Behav Brain Res. 1997;89:267–273. - PubMed
-
- Carrozzo M, McIntyre J, Zago M, Lacquaniti F. Viewer-centered and body-centered frames of reference in direct visuomotor transformations. Exp Brain Res. 1999;129:201–210. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
