Long-range temporal correlations and scaling behavior in human brain oscillations

Abstract

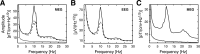
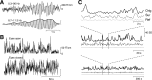
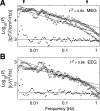
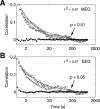
The human brain spontaneously generates neural oscillations with a large variability in frequency, amplitude, duration, and recurrence. Little, however, is known about the long-term spatiotemporal structure of the complex patterns of ongoing activity. A central unresolved issue is whether fluctuations in oscillatory activity reflect a memory of the dynamics of the system for more than a few seconds. We investigated the temporal correlations of network oscillations in the normal human brain at time scales ranging from a few seconds to several minutes. Ongoing activity during eyes-open and eyes-closed conditions was recorded with simultaneous magnetoencephalography and electroencephalography. Here we show that amplitude fluctuations of 10 and 20 Hz oscillations are correlated over thousands of oscillation cycles. Our analyses also indicated that these amplitude fluctuations obey power-law scaling behavior. The scaling exponents were highly invariant across subjects. We propose that the large variability, the long-range correlations, and the power-law scaling behavior of spontaneous oscillations find a unifying explanation within the theory of self-organized criticality, which offers a general mechanism for the emergence of correlations and complex dynamics in stochastic multiunit systems. The demonstrated scaling laws pose novel quantitative constraints on computational models of network oscillations. We argue that critical-state dynamics of spontaneous oscillations may lend neural networks capable of quick reorganization during processing demands.

Fig. 1.

DFA quantifies correlations in nonstationary patchy signals. A, The amplitude at 10 Hz is shown for a typical occipital MEG channel during eyes-closed for the entire 1200 sec. The first step of the DFA is to subtract the mean value of the signal (A) and then compute the cumulative sum of the signal (B).C, The integrated signal is detrended at all time scales by selecting a time interval (window), here shown for a 120 sec window, fitting a least-squares line to the interval and subtracting the linear trend (D). E, The average of the root-mean-square fluctuation of the entire integrated and detrended signal is computed for the window size 120 sec and plotted in double-logarithmic coordinates (see arrow). The procedure starting in C is repeated for several window sizes to give the data points in E, and the power-law exponent is the slope of the line fitted to the data points in the interval marked by the two arrowheads. The lower bound of the fitting range was chosen as the shortest time window that did not show temporal correlations induced by the wavelet filtering. The upper bound was empirically determined as the maximum window size that would not include large outliers resulting from the poor statistics at large window sizes.

Fig. 2.

Amplitude spectra of MEG and EEG signals. Grand average (n = 10) amplitude spectra of conditions eyes-closed (thick solid line) and eyes-open (thick dashed line) display large peaks in the alpha frequency band (8–13 Hz) for selected channels in the occipitoparietal region of MEG (A) and EEG (B). C, Pronounced mu (8–13 Hz) and beta (15–25 Hz) activity was present in 9 of 10 subjects over the right somatosensory region (eyes-closed). Amplitude spectra of an MEG recording with no subject present are shown (“reference recording;”thin lines) to give an impression of the average signal-to-noise ratio of the MEG signals.

Fig. 3.

Alpha oscillations, dominating the spontaneous activity, fluctuate in amplitude on a wide range of time scales.A, MEG signal from the occipital region and the eyes-open condition. The 4 sec epoch of broadband MEG (0.3–90 Hz;top curve) displays a typical transition from low alpha activity to large-amplitude 10 Hz oscillations (bottomcurve). The thick line of thebottom curve indicates the amplitude envelope of the bandpass-filtered signal (8.7–11.3 Hz) obtained with the wavelet filter. B, Continuous and pronounced fluctuations in the alpha oscillation amplitude are seen in 150 sec epochs from conditions eyes-open (top curve) and eyes-closed (bottom curve). C, Signals, wavelet-filtered at 10 Hz, are displayed for original eyes-open data (Orig), surrogate data (Sur), and the reference recording (Ref). To visualize fluctuations at different magnifications (see time scales), the signals were down-sampled to 15 Hz (top three curves), 1.5 Hz (middle curves), and 0.15 Hz (bottomcurves). The amplitude scale is the same for all curves and is given in SDs of the reference recording. The amplitude fluctuations at time scales of a couple of seconds are clearly above the noise level of the sensors but fluctuate similarly to the surrogate data. At time scales of tens or hundreds of seconds, the variations of alpha oscillations at all scales is revealed in the tendency of the original signal to preserve larger amplitudes and amplitude variability than the surrogate signal.

Fig. 4.

Alpha oscillations show 1/f-like power spectra for their amplitude modulation. The grand averaged (n = 10) power spectral density of alpha rhythm amplitude fluctuations is plotted in double-logarithmic coordinates for MEG (A) and EEG (B) data.Circles, Eyes-closed condition. Crosses, Eyes-open condition. The dots represent the reference recording and the surrogate data for the MEG and EEG power spectra, respectively. Arrowheads mark the interval used for estimation of slopes (see Materials and Methods).

Fig. 5.

Alpha oscillations have statistically significant correlations at time lags >100 sec. The grand averaged (n = 10) autocorrelation functions of alpha rhythm amplitude fluctuations exhibit a power-law decrease in correlation with increasing time lag for both MEG (A) and EEG (B) data. The abscissas are logarithmic, and thesolid lines are power-law fits to the data.Circles, Eyes-closed condition. Crosses, Eyes-open condition. The autocorrelations of the reference recording and surrogate data are effectively zero at all time lags (dots). The significance of the correlations compared with zero is indicated for the time lag of nearly 200 sec.

Fig. 6.

Alpha oscillations exhibit robust power-law scaling behavior and long-range temporal correlations. Double-logarithmic plots of the DFA fluctuation measure,F(τ), show power-law scaling in the time window range of 5–300 sec for both MEG (A) and EEG (B) data. Circles, Eyes-closed condition. Crosses, Eyes-open condition. Thedots represent reference recording and surrogate data for the MEG and EEG, respectively. C, Scatter plots of mean oscillation amplitude and DFA scaling exponents show no (eyes-open condition, crosses) or slight negative correlation (eyes-closed condition, circles). D, Scatter plots of scaling versus amplitude ratios (NS). Note the large variability across subjects for the amplitude ratios relative to the scaling ratios. All lines are least-squares fits to the data.

Fig. 7.

Somatosensory mu and beta oscillations exhibit robust power-law scaling behavior and long-range temporal correlations.A, Double-logarithmic plots of the DFA fluctuation measure, F(τ), as a function of window size, τ, display power-law scaling in the time window range of 5–300 sec of mu (circles) and beta (asterisks) oscillations during the eyes-closed condition. The fitting interval is indicated with arrowheads. The dotsrepresent a reference recording wavelet-filtered at 20 Hz.B, The autocorrelation function of the mu (circles) and beta (asterisks) rhythms.C, Scatter plots of mean oscillation amplitude versus DFA scaling exponents (left) and amplitude ratios versus scaling ratios (right).