Colored noise and computational inference in neurophysiological (fMRI) time series analysis: resampling methods in time and wavelet domains

Abstract

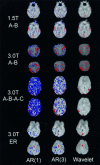
Even in the absence of an experimental effect, functional magnetic resonance imaging (fMRI) time series generally demonstrate serial dependence. This colored noise or endogenous autocorrelation typically has disproportionate spectral power at low frequencies, i.e., its spectrum is (1/f)-like. Various pre-whitening and pre-coloring strategies have been proposed to make valid inference on standardised test statistics estimated by time series regression in this context of residually autocorrelated errors. Here we introduce a new method based on random permutation after orthogonal transformation of the observed time series to the wavelet domain. This scheme exploits the general whitening or decorrelating property of the discrete wavelet transform and is implemented using a Daubechies wavelet with four vanishing moments to ensure exchangeability of wavelet coefficients within each scale of decomposition. For (1/f)-like or fractal noises, e.g., realisations of fractional Brownian motion (fBm) parameterised by Hurst exponent 0 < H < 1, this resampling algorithm exactly preserves wavelet-based estimates of the second order stochastic properties of the (possibly nonstationary) time series. Performance of the method is assessed empirically using (1/f)-like noise simulated by multiple physical relaxation processes, and experimental fMRI data. Nominal type 1 error control in brain activation mapping is demonstrated by analysis of 13 images acquired under null or resting conditions. Compared to autoregressive pre-whitening methods for computational inference, a key advantage of wavelet resampling seems to be its robustness in activation mapping of experimental fMRI data acquired at 3 Tesla field strength. We conclude that wavelet resampling may be a generally useful method for inference on naturally complex time series.

Figure 1

Daubechies mother ψ and father ϕ wavelets with four vanishing moments and local support over eight time points. This is the basis adopted for resampling of time series in the wavelet domain because this number of vanishing moments is sufficient to decorrelate the wavelet coefficients of fractal noises with Hurst exponent H < 1; Daubechies wavelets have minimum local support for any given number of vanishing moments; and compactness of support minimises artefactual intercoefficient correlations due to boundary correction in finite time series.

Figure 2

Synthesis, analysis, and resampling of fractional Brownian motion (fBm). Top row: Expected autocovariance matrices Ω_B for fBm with Hurst exponents H = 0.5 and H = 0.25. Second row: Fractional Brownian processes (N = 128) realised by coloring a normal white process ϵ with the Cholesky factor of Ω_B, see Eq 12. Third row: Empirical estimation of Hurst exponents by least squares fit of Eq 21. The slope of the straight line drawn through the five points in each plot of level j (on the x‐axis) vs. log variance of wavelet coefficients (on the y‐axis) equals 2Ĥ + 1. Fourth row: fBm resampled by random permutation of the wavelet coefficients of the simulated series. The Hurst exponents estimated by Eq 21, Ĥ = 0.45 and 0.23, are identical for the simulated and resampled series.

Figure 3

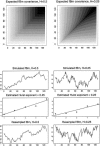
Wavelet resampling of simulated ${}_{\stackrel{\text{–}}{\mathit{\text{f}}}}^{\text{1}}$‐like noise. Top row, from left to right: A time series simulated by a physical model of multiple relaxation processes (N = 128); its autocorrelation function (ACF), with dashed lines indicating Bartlett's 95% confidence interval for zero, 0 ± 2/ ; and its discrete wavelet transform (DWT). The coefficients of the dilated and translated mother wavelets are shown for five levels of detail j, labelled d1–d5; and for the father wavelet, labelled s5. The top row of this panel shows the time series reconstructed by the inverse wavelet transform. Middle row, from left to right: The autocorrelation functions of the wavelet coefficients at levels d1–d3 are shown with dashed lines indicating 95% CI for zero, 0 ± 2/ . 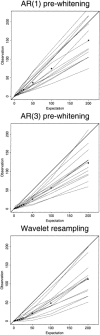Bottom row, right to left: The wavelet coefficients after random permutation within each level of detail; the autocorrelation function of the time series obtained by the inverse wavelet transform on the resampled coefficients; the resampled time series. The key point is that although the original time series is significantly autocorrelated, its wavelet coefficients are relatively whitened or decorrelated, and random permutation of these serially independent or exchangeable coefficients generates a resampled time series with an autocorrelation function very similar to the original.

Figure 4

Wavelet resampling of fractal noise simulated by multiple relaxation processes. The mean (dashed line) and 95% confidence envelope (black shading) for the autocorrelation function estimated over 50 realisations of ${}_{\stackrel{\text{–}}{\mathit{\text{f}}}}^{\text{1}}$‐like noise (N = 128) can be compared to the mean (solid line) and 95% confidence envelope (dark grey shading) for the autocorrelation function estimated over 50 resamples of a single simulated series. The area of the ACF envelopes common to both simulated and resampled series is shaded pale grey. Evidently the resampling scheme mimics closely the mean and variability of autocorrelational structure in the multiple simulated series.

Figure 5

Wavelet resampling of functional MRI noise. Top: A functional MRI time series observed under resting or null conditions at 1.5 Tesla (N = 128). Bottom row, left: Autocorrelation function of observed fMRI series. Bottom row, right: The observed (dashed line) autocorrelation function can be compared to the mean (solid line) and 95% confidence envelope (grey shading) for the autocorrelation function estimated over 50 resamples of the observed fMRI series. The observed autocorrelation function lies within the 95% confidence envelope estimated by (apparently unbiased) wavelet resampling.

Figure 6

Type 1 error calibration curves for time domain resampling schemes based on AR(1) and AR(3) pre‐whitening by the Cochrane‐Orcutt procedure, and for wavelet domain resampling. In each plot of the observed number of positive tests vs. the expected number of positive tests, each of the dotted lines represents the results for one of 13 images acquired under null or resting conditions; the points represent the observed number of positive tests averaged over images; and the solid line y = x indicates perfect agreement between observation and expectation. For a valid test, the observed number of positive tests under the null hypothesis must be less than or equal to the expected number. By this criterion all three tests are valid on average; but AR(3) pre‐whitening and wavelet resampling are also valid for each of the individual images.

Figure 7

Brain activation mapping of experimental fMRI data based on different treatments of residual autocorrelation: AR(1) pre‐whitening, middle row AR(3) pre‐whitening, bottom row wavelet resampling. 1.5T AB two‐condition periodically designed data acquired at 1.5T; 3.0T AB two‐condition periodically designed data acquired at 3.0T (Cambridge); 3.0T ABAC three‐condition periodically designed data acquired at 3.0T (Oxford); 3.0T ER event‐related data acquired at 3.0T (Oxford). In all maps, red voxels indicate significant activation with voxel‐wise probability of type 1 error P < 1 × 10⁻³; blue voxels indicate where the “pre‐whitened” regression model residuals were not in fact serially independent by the Box‐Pierce test. The key point to note is that wavelet resampling is considerably more robust than the pre‐whitening schemes in dealing with some of the higher field datasets, but of approximately equivalent sensitivity.