Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms

Abstract

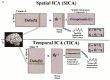
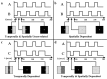
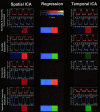
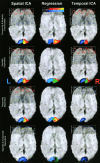
Independent component analysis (ICA) is a technique that attempts to separate data into maximally independent groups. Achieving maximal independence in space or time yields two varieties of ICA meaningful for functional MRI (fMRI) applications: spatial ICA (SICA) and temporal ICA (TICA). SICA has so far dominated the application of ICA to fMRI. The objective of these experiments was to study ICA with two predictable components present and evaluate the importance of the underlying independence assumption in the application of ICA. Four novel visual activation paradigms were designed, each consisting of two spatiotemporal components that were either spatially dependent, temporally dependent, both spatially and temporally dependent, or spatially and temporally uncorrelated, respectively. Simulated data were generated and fMRI data from six subjects were acquired using these paradigms. Data from each paradigm were analyzed with regression analysis in order to determine if the signal was occurring as expected. Spatial and temporal ICA were then applied to these data, with the general result that ICA found components only where expected, e.g., S(T)ICA "failed" (i.e., yielded independent components unrelated to the "self-evident" components) for paradigms that were spatially (temporally) dependent, and "worked" otherwise. Regression analysis proved a useful "check" for these data, however strong hypotheses will not always be available, and a strength of ICA is that it can characterize data without making specific modeling assumptions. We report a careful examination of some of the assumptions behind ICA methodologies, provide examples of when applying ICA would provide difficult-to-interpret results, and offer suggestions for applying ICA to fMRI data especially when more than one task-related component is present in the data.

Figure 1

Visual depiction of SICA and TICA of fMRI. The matrix representation of the SICA (a) and TICA (b) approaches. In each case, the spatial information is flattened into one dimension and the temporal information is one dimension. In SICA, the algorithm attempts to find spatially independent components with associated (unconstrained) time courses whereas in TICA the algorithm attempts to find temporally independent time courses with associated spatial maps.

Figure 2

Graphical depiction of paradigms. The same basic paradigms were used for both the simulations and the fMRI experiments. The time courses represent the 6‐min experiment and the squares illustrate what the subjects were seeing in the scanner at each indicated time. The simulated data was created by adding the represented time courses (after convolution with a hemodynamic response function) to random noise.

Figure 3

Results of analyses of simulated data. Thresholded activation maps are overlaid on a gray square using colors as follows: red corresponding to areas that produced the red time course, blue for areas that produced the blue time course, and green indicating areas that matched both time courses. Figures are arranged in a 3‐by‐4 grid where columns are SICA, regression, and TICA results, respectively, and rows are successive experiments. Note that SICA was “successful” in extracting the true answer in experiments (a) and (c), whereas TICA was “successful” in extracting the true answer in experiments (a) and (b). Regression was successful in all cases (to be expected since the exact model is known).

Figure 4

Results of analyses of fMRI data (one subject). Thresholded activation maps for one slice are overlaid on the EPI image using colors as follows: red corresponding to areas that produced the red time course, blue for areas that produced the blue time course, and green indicating areas that matched both time courses. Figures are arranged in a 3‐by‐4 grid where columns are SICA, regression, and TICA results, respectively, and rows are successive experiments. Note that SICA agreed with the regression results in experiments (a) and (c), whereas TICA agreed with the regression results in experiments (a) and (b).