A critical investigation of the Tanford-Kirkwood scheme by means of Monte Carlo simulations

Abstract

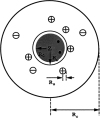
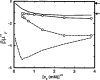
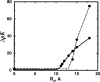
Monte Carlo simulations are used to assess the adequacy of the Tanford-Kirkwood prescription for electrostatic interactions in macromolecules. Within a continuum dielectric framework, the approach accurately describes salt screening of electrostatic interactions for moderately charged systems consistent with common proteins at physiological conditions. The limitations of the Debye-Hückel theory, which forms the statistical mechanical basis for the Tanford-Kirkwood result, become apparent for highly charged systems. It is shown, both by an analysis of the Debye-Hückel theory and by numerical simulations, that the difference in dielectric permittivity between macromolecule and surrounding solvent does not play a significant role for salt effects if the macromolecule is highly charged. By comparison to experimental data, the continuum dielectric model (combined with either an approximate effective Hamiltonian as in the Tanford-Kirkwood treatment or with exact Monte Carlo simulations) satisfactorily predicts the effects of charge mutation on metal ion binding constants, but only if the macromolecule and solvent are assigned the same or similar permittivities.

Fig. 1.

Schematic representation of the model systems (see also Table 1). A spherical protein in a spherical cell with radii R_p and R_C, respectively. The protein interior with a low dielectric permittivity is shown as a shaded region of radius R_d < R_p. A central charge of valency Z and two binding sites marked as black dots.

Fig. 2.

The reduced excess chemical potential for a free divalent cation in a 20 μM protein solution is indicated as a function of monovalent salt concentration. The (superimposed) solid lines refer to the SC8 model and the broken lines to the SC24 model. Lines marked by solid circles are calculated with a dielectric boundary radius R_d = 14Å; lines without symbols refer to R_d = 0Å. The thin broken line shows the excess chemical potential of a divalent ion in a bulk salt solution.

Fig. 3.

The reduced excess chemical potential for a divalent cation as a function of protein concentration with a homogeneous dielectric response (dielectric radius R_d = 0). The solid lines refer to the SC8 model and the broken lines to the SC24 model. Lines marked by circles denote a monovalent simple electrolyte concentration of c_s = 100 mM; lines without symbols are for c_s = 1 mM. The arrows indicate the value of βμ_F^ex in the corresponding bulk salt solutions. The upper arrow indicates the system at c_s = 1 mM (βμ_F^ex = −0.156).

Fig. 4.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC8 model. A reference state at c_s = 1 mM is chosen and the protein is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 18Å and those marked by open squares denote R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å). (b) The shift of ΔpK arising from the presence of an interior vacuum ΔΔpK = ΔpK (R_d = 0Å) − ΔpK (R_d = 14Å) is demonstrated as a function of salt concentration c_s. In the solvent region, the relative dielectric permittivity is ɛ_s = 78.7. Solid line shows MC data and broken line indicates TK results. (c) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for a spherical protein model with eight randomly placed negative charges. Results from MC simulations and TK calculations are compared as solid line and solid circles, respectively. The protein dielectric boundary radius was R_d = 12Å in all calculations.

Fig. 4.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC8 model. A reference state at c_s = 1 mM is chosen and the protein is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 18Å and those marked by open squares denote R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å). (b) The shift of ΔpK arising from the presence of an interior vacuum ΔΔpK = ΔpK (R_d = 0Å) − ΔpK (R_d = 14Å) is demonstrated as a function of salt concentration c_s. In the solvent region, the relative dielectric permittivity is ɛ_s = 78.7. Solid line shows MC data and broken line indicates TK results. (c) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for a spherical protein model with eight randomly placed negative charges. Results from MC simulations and TK calculations are compared as solid line and solid circles, respectively. The protein dielectric boundary radius was R_d = 12Å in all calculations.

Fig. 4.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC8 model. A reference state at c_s = 1 mM is chosen and the protein is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 18Å and those marked by open squares denote R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å). (b) The shift of ΔpK arising from the presence of an interior vacuum ΔΔpK = ΔpK (R_d = 0Å) − ΔpK (R_d = 14Å) is demonstrated as a function of salt concentration c_s. In the solvent region, the relative dielectric permittivity is ɛ_s = 78.7. Solid line shows MC data and broken line indicates TK results. (c) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for a spherical protein model with eight randomly placed negative charges. Results from MC simulations and TK calculations are compared as solid line and solid circles, respectively. The protein dielectric boundary radius was R_d = 12Å in all calculations.

Fig. 5.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC24 model. Other details are as for Fig. 4A ▶. (b) The difference of excess chemical potentials βΔμ_B^ex = βμ_B^ex(c_s) − βμ_B^ex(c_s = 1 mM) for a divalent cation in a bulk monovalent electrolyte solution is plotted as a function of salt concentration c_s.

Fig. 5.

(a) Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of salt concentration c_s for the SC24 model. Other details are as for Fig. 4A ▶. (b) The difference of excess chemical potentials βΔμ_B^ex = βμ_B^ex(c_s) − βμ_B^ex(c_s = 1 mM) for a divalent cation in a bulk monovalent electrolyte solution is plotted as a function of salt concentration c_s.

Fig. 6.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the protein net charge (Z). A reference state at salt concentration c_s = 1 mM is chosen and the final salt concentration is 500 mM. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively. Lines marked by solid circles correspond to a dielectric boundary radius R_d = 12Å; unmarked lines refer to a homogeneous dielectric response (R_d = 0Å).

Fig. 7.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the dielectric radius R_d for the SC8 model. A reference state at salt concentration c_s = 1 mM is chosen and the protein (of radius R_p = 14Å) is allowed to bind two divalent cations. Results from MC simulations and TK calculations are compared as solid and broken lines, respectively.

Fig 8.

Total shift in ion binding constant ΔpK, owing to solution ionic strength, is plotted as a function of the dielectric radius R_d for the SC24 model. A reference state at salt concentration c_s = 1 mM is chosen and the protein (of radius Rp = 14Å) is allowed to bind two divalent cations. The final salt concentration is 500 mM. Results from MC simulations and TK calculations are compared as open and solid symbols, respectively, joined by straight line segments to guide the eye.

Fig. 9.

Total shift in ion binding constant ΔpK, owing to a single charge mutation, is plotted as a function of the dielectric radius R_d for the SC8 and SP8 models. The salt concentration is c_s = 1 mM and the protein concentration is c_p = 0.02 mM. MC results are shown with solid (SC8) and broken (SP8) lines; TK data are denoted by solid circles.