Intrinsic noise in gene regulatory networks
- PMID: 11438714
- PMCID: PMC37484
- DOI: 10.1073/pnas.151588598
Intrinsic noise in gene regulatory networks
Abstract
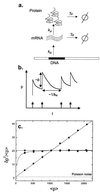
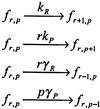
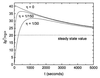
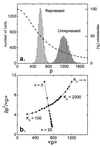
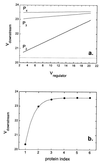
Cells are intrinsically noisy biochemical reactors: low reactant numbers can lead to significant statistical fluctuations in molecule numbers and reaction rates. Here we use an analytic model to investigate the emergent noise properties of genetic systems. We find for a single gene that noise is essentially determined at the translational level, and that the mean and variance of protein concentration can be independently controlled. The noise strength immediately following single gene induction is almost twice the final steady-state value. We find that fluctuations in the concentrations of a regulatory protein can propagate through a genetic cascade; translational noise control could explain the inefficient translation rates observed for genes encoding such regulatory proteins. For an autoregulatory protein, we demonstrate that negative feedback efficiently decreases system noise. The model can be used to predict the noise characteristics of networks of arbitrary connectivity. The general procedure is further illustrated for an autocatalytic protein and a bistable genetic switch. The analysis of intrinsic noise reveals biological roles of gene network structures and can lead to a deeper understanding of their evolutionary origin.
Figures
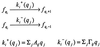

References
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

