The dissociation of acetylcholine from open nicotinic receptor channels

Abstract

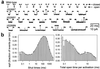
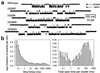
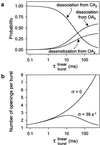
Ligand-gated ion channels bind agonists with higher affinity in the open than in the closed state. The kinetic basis of this increased affinity has remained unknown, because even though the rate constants of agonist association to and dissociation from closed receptors can be estimated with reasonable certainty, the kinetics of the binding steps in open receptors have proven to be elusive. To be able to measure the agonist-dissociation rate constant from open muscle nicotinic receptors, we increased the probability of ligand unbinding from the open state by engineering a number of mutations that speed up opening and slow down closing but leave the ligand-binding properties unchanged. Single-channel patch-clamp recordings from the wild-type and mutant constructs were performed at very low concentrations of acetylcholine (ACh). The durations of individual channel activations were analyzed assuming that "bursts" of fully liganded (diliganded) receptor openings can be terminated by ligand dissociation from the closed or open state (followed by fast closure) or by desensitization. This analysis revealed that ACh dissociates from diliganded open receptors at approximately 24 s(-1), that is, approximately 2,500 times more slowly than from diliganded closed receptors. This change alone without a concomitant change in the association rate constant to the open state quantitatively accounts for the increased equilibrium affinity of the open channel for ACh. Also, the results predict that both desensitization and ACh dissociation from the open state frequently terminate bursts of openings in naturally occurring gain-of-function mutants (which cause slow-channel congenital myasthenia) and therefore would contribute significantly to the time course of the endplate current decay in these disease conditions.

Figure 1

A Monod–Wyman–Changeux type of model (1) for the muscle AChR. C, O, and D denote the closed, open, and desensitized conformations, respectively, and A denotes the agonist concentration. Under equilibrium conditions, the net free-energy change around a “thermodynamic cycle” is zero. Therefore, the product of the equilibrium constants around each loop in this model is constrained to be unity (principle of detailed balance). This leads to the calculation that the affinity of the open state (j₊/j₋) is larger than that of the closed state (k₊/k₋) by a factor of . In the case of the wild-type AChR and all the mutant constructs having wild-type ligand-binding properties, this factor is ≈1,500–5,000 in the presence of ACh. The model is appropriate as far as gating (occurring as a one-step reaction) and desensitization of diliganded receptors (proceeding from the open state) are concerned. It is clear, however, that there is more than one desensitized state (Fig. 4 and refs. and 6), and it is not known whether the mono- and unliganded D states are connected directly to the open, closed, or both states (hence, the dashed arrows; ref. 7). Nevertheless, none of these uncertainties and simplifications compromise the conclusions of this work. Once the channel reaches the OA₂ state (from CA₂, OA, or DA₂), it can close and reopen repeatedly (OA₂ ⇋ CA₂). If the concentration of ligand is sufficiently low and the rate constant of the DA₂ → OA₂ transition is much slower than that of DA₂ → DA, these bursts of openings will continue until the ligand dissociates from CA₂ or OA₂ (followed by closure) or until the channel desensitizes. We refer to the mean number of sojourns in OA₂ per burst as the “number of openings per burst.” The five rate constants that determine the time constant of the slowest component of the burst-length distribution at very low concentrations of agonist (Eq. 2), and thus that would shape the time course of the endplate current decay (8, 9), are indicated in bold.

Figure 2

Single-channel activations and the estimation of τ_burst values. (a) Bursts of openings excised from continuous single-channel recordings elicited by low concentrations of ACh (5 μM for the wild-type and 100 nM for the other three constructs) at ≈ −100 mV in the cell-attached configuration. Some of the open periods were interrupted by short but well defined gaps (0.355-ms component in the example shut-time histogram of b), some of which are indicated with asterisks. These, and other less well defined shut intervals also present in the figure (48-μs component in the example below) most likely correspond to dwellings in nonconductive diliganded states other than the very brief CA₂ (mean lifetime < 10 μs). Sojourns in these “extra” states were ignored by concatenating the flanking open intervals (see Materials and Methods). Display bandwidth, dc to 6 kHz. Openings are downward deflections. (b) Dwell-time histograms of an example patch of a cell expressing the δS268N mutant. The shut-time histogram, which includes all the shut intervals in the record, was best fitted (maximum likelihood method) with a mixture of five exponential densities with means of 48 μs (5%), 0.355 ms (3%), 32.1 ms (21%), 141 ms (60%), and 430 ms (11%); 5,543 events were included in the fit. The total-open-time-per-activation histogram (see Materials and Methods) was best fitted with a mixture of three exponential densities with means of 60 μs (41%), 0.276 ms (51%), and 14.9 ms (8%); 5,051 events were included in the fit. We refer to the time constant of the slowest component of this distribution as τ_burst. The intermediate and fastest components correspond, to a very good approximation, to isolated monoliganded and unliganded openings, respectively.

Figure 3

σ value estimation. (a) Plot of experimental τ_burst values as a function of the opening and closing rate constants. The values of τ_burst, β₂, and α₂ for each construct in the presence of ACh are shown in Table 1. The fit with Eq. 2 (least squares method) yielded estimates of 2k₋ = 56,870 ± 17,310 s⁻¹ and σ = 39 ± 9 s⁻¹ (mean ± SD). The vertical lines denote the distance between each experimental point and the fitted surface. The points corresponding to the δS→Q and the βT→S + δS→T + ɛT→S mutants are not displayed. (b) A lower magnification version of the plot in a. (c) Plot of τ_burst (mean ± SD) as a function of τ. τ values (Eq. 1) were calculated for each construct by using the values of β₂ and α₂ in Table 1 and the estimated 2k₋ value of 56,870 s⁻¹. The fit with Eq. 2 (least squares method) yielded σ = 39 ± 4 s⁻¹ (mean ± SD). This fit predicts a maximum τ_burst value of 1/σ = 25.6 ms. The δS→Q and βT→S + δS→T + ɛT→S (“triple”) mutants were deemed outliers and were excluded from the fit. Most likely, the affinities for ACh in the closed and/or open states are altered in these two constructs (Fig. 4). The dashed straight line is the prediction of models that ignore desensitization and ligand dissociation from the open state (e.g., refs. , , and 25). That is, from Eq. 2, if σ = 0, then τ = τ. Because σ is actually different from zero, desensitization and ligand dissociation from the open state can cut bursts short and thus can shape the time course of the endplate current decay.

Figure 4

The rate of entry into desensitization. (a) Clusters of single-channel activity recorded at 100 μM ACh and ≈ −100 mV were used to estimate the rate of entry into desensitization, k_+D (as defined in Materials and Methods). At this high concentration of ACh, binding is so fast that sojourns in the closed state are very short lived. Hence, most of the longer lived shut intervals correspond to visits to a number of desensitized states. The average value for the tested constructs (Thr, Ile, Asn, and Gln mutants) was k_+D = 14.8 ± 6.0 s⁻¹ (mean ± SD, 4 constructs, 15 patches). The wild-type's data were not included in this calculation, because the longer lived closures at 100 μM ACh (see traces) precluded a clear identification of the gap component (see Materials and Methods). The kinetics of entry into desensitization were not affected greatly in the outlier construct δS→Q (k_+D = 11.4 ± 3.2 s⁻¹, mean ± SD, 5 patches) suggesting that this mutation most likely affects the ligand-binding properties of the channel. Display bandwidth, dc to 6 kHz. Openings are downwards. (b) Dwell-time histograms of an example patch of a cell expressing the δS268Q mutant. The shut-time histogram, which includes all of the shut intervals in the record, was best fitted (maximum likelihood method) with a mixture of six exponential densities with means of 20 μs (70%), 0.134 ms (20%), 0.711 ms (6%), 6.3 ms (2%), 88 ms (1%), and 1.5 s (1%). 8,750 events were included in the fit. The total-open-time-per-cluster histogram (see Materials and Methods) was best fitted with a mixture of two exponential densities with means of 82 μs (20%) and 92 ms (80%); 458 events were included in the fit. The reciprocal of the time constant of the longest component gives the k_+D value. The short lived component corresponds to isolated openings present even at concentrations as high as 100 μM ACh.

Figure 5

Properties of bursts of diliganded openings. (a) The probability of a burst being terminated by ligand dissociation from the open state (followed by closure), desensitization, or ligand dissociation from the closed state were calculated as 2j₋τ, k_+Dτ, and 1 − στ, respectively, where τ is given by Eq. 2, and σ = 2j₋ + k_+D. The values of 2j₋ and k_+D were taken as 24 and 25 s⁻¹, respectively. (b) It is difficult, or even impossible, to count the number of openings per burst in constructs that open at wild type or even higher rates (>50,000 s⁻¹), because sojourns in the closed diliganded state, CA₂, are too short (<10 μs on average) to be fully detected. However, in the framework of the kinetic scheme in Fig. 1, this number can be calculated as (σ + α₂)τ. For the δ12′ mutant series and in the hypothetical case of σ = 0, this number increases continuously. With σ = 39 s⁻¹, however, this number goes through a maximum of ≈2.6 openings and tends to 1 at limiting large values of τ. These calculations are not heavily model-dependent; they are based only on the notion that AChRs can open and close, that desensitization of diliganded receptors proceeds predominantly from the open state, and that the ligand can dissociate from both the closed and open conformations.