Comparison of a hair bundle's spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process
- PMID: 11724945
- PMCID: PMC64690
- DOI: 10.1073/pnas.251530598
Comparison of a hair bundle's spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process
Abstract
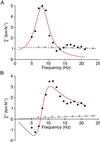
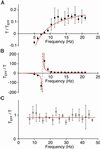
Hearing relies on active filtering to achieve exquisite sensitivity and sharp frequency selectivity. In a quiet environment, the ears of many vertebrates become unstable and emit one to several tones. These spontaneous otoacoustic emissions, the most striking manifestation of the inner ear's active process, must result from self-sustained mechanical oscillations of aural constituents. The mechanoreceptive hair bundles of hair cells in the bullfrog's sacculus have the ability to amplify mechanical stimuli and oscillate spontaneously. By comparing a hair bundle's spontaneous oscillations with its response to small mechanical stimuli, we demonstrate a breakdown in a general principle of equilibrium thermodynamics, the fluctuation-dissipation theorem. We thus confirm that a hair bundle's spontaneous movements are produced by energy-consuming elements within the hair cell. To characterize the dynamical behavior of the active process, we introduce an effective temperature that, for each frequency component, quantifies a hair bundle's deviation from thermal equilibrium. The effective temperature diverges near the bundle's frequency of spontaneous oscillation. This behavior, which is not generic for active oscillators, can be accommodated by a simple model that characterizes quantitatively the fluctuations of the spontaneous movements as well as the hair bundle's linear response function.
Figures
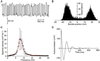
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

