Bias in estimates of quantitative-trait-locus effect in genome scans: demonstration of the phenomenon and a method-of-moments procedure for reducing bias

Abstract

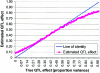
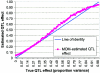
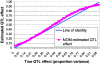
An attractive feature of variance-components methods (including the Haseman-Elston tests) for the detection of quantitative-trait loci (QTL) is that these methods provide estimates of the QTL effect. However, estimates that are obtained by commonly used methods can be biased for several reasons. Perhaps the largest source of bias is the selection process. Generally, QTL effects are reported only at locations where statistically significant results are obtained. This conditional reporting can lead to a marked upward bias. In this article, we demonstrate this bias and show that its magnitude can be large. We then present a simple method-of-moments (MOM)-based procedure to obtain more-accurate estimates, and we demonstrate its validity via Monte Carlo simulation. Finally, limitations of the MOM approach are noted, and we discuss some alternative procedures that may also reduce bias.

Figure 1

Estimated versus true QTL effects, without selection of only significant results. All analyses included 200 independent sibling pairs and used HE2 to provide the QTL estimates.

Figure 2

Estimated versus true QTL effects, with selection of only significant results. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

Figure 3

MOM estimates of QTL effect versus true QTL effect, with selection of only significant results from experiment 2. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

Figure 4

MOM estimates of QTL effect versus true QTL effect, with selection of only significant results from experiment 3. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

Figure 5

Simulations with nonadditive models, but with MOM estimates calculated assuming additivity. Note that the true QTL effects, as well as the preliminary (ordinary) estimates, include both the additive component and the dominance component. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01. For details of nonadditive models, see the “Simulation Parameters and Methods” subsection.