Single ion occupancy and steady-state gating of Na channels in squid giant axon

Abstract

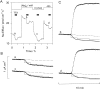
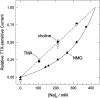
The properties of the small fraction of tetrodotoxin (TTX)-sensitive Na channels that remain open in the steady state were studied in internally dialyzed voltage clamped squid giant axons. The observed Ussing flux ratio exponent (n') of 0.97 plus minus 0.03 (calculated from simultaneous measurements of TTX-sensitive current and (22)Na efflux) and nonindependent behavior of Na current at high internal [Na] are explained by a one-site ("1s") permeation model characterized by a single effective binding site within the channel pore in equilibrium with internal Na ions (apparent equilibrium dissociation constant K(Nai)(0) = 0.61 +/- 0.08 M). Steady-state open probability of the TTX-sensitive channels can be modeled by the product p(a)p(infinity), where p(a) represents voltage-dependent activation described by a Boltzmann distribution with midpoint V(a) = -7 mV and effective valence z(a) = 3.2 (Vandenberg, C.A., and F. Bezanilla. 1991. BIOPHYS: J. 60:1499--1510) coupled to voltage-independent inactivation by an equilibrium constant (Bezanilla, F., and C.M. Armstrong. 1977. J. Gen. Physiol. 70:549--566) K(eq) = 770. The factor p(infinity) represents voltage-dependent inactivation with empirical midpoint V(infinity)= -83 plus minus 5 mV and effective valence z(infinity) = 0.55 plus minus 0.03. The composite p(a)p(infinity)1s model describes the steady-state voltage dependence of the persistent TTX-sensitive current well.

Figure 1.

Equality of TTX-sensitive ²²Na efflux and current in Na-free extracellular solution. An axon internally dialyzed with 50 mM Na and 0.25 mM veratridine and superfused with Na-free, 10-mM K solution was clamped initially at −60 mV. (a) Addition of 10 μM dihydrodigitoxigenin (H₂DTG, a specific Na/K pump blocker) caused Na efflux to decrease by 34.6 pmol cm⁻² s⁻¹ and outward current by 1.0 μA cm⁻², which yields a pump-mediated Na efflux-to-current ratio of 3.3, which is compatible with the value of 3.0 expected for a 3 Na/2 K stoichiometry (Rakowski et al., 1989). Changing the holding potential to 0 mV in the continued presence of H₂DTG (and internal veratridine) elicited a large Na efflux, which then declined exponentially with a time constant of 4.00 ± 0.11 min. (b) Addition of 0.2 μM TTX caused Na efflux to decrease by 38.5 pmol cm⁻² s⁻¹ and outward current by 3.68 μA cm⁻², yielding a TTX-sensitive Na efflux-to-current (FΔΦ_out/ΔI) ratio of 1.01. (c) Washout of H₂DTG allowed recovery of 34.l pmol cm⁻² s⁻¹ of Na/K pump-mediated Na efflux.

Figure 8.

Determination of the flux ratio exponent n′. (A) An axon held at −30 mV and internally dialyzed with 200 mM radiolabeled Na was repeatedly exposed to 0.2 μM TTX in 425 mM choline, Na-free solution (a and c) or in 425 mM Na, choline-free solution (b and d). (B) The two TTX induced ²²Na efflux drops in Na-free (choline) solution (a and c) are replotted on expanded time bases and scaled by Faraday's constant, together with the TTX-induced shifts in holding current recorded at the same time. (C) Comparison of current transients b and d (also on expanded time bases) with the simultaneously measured drop in ²²Na efflux. TTX addition in the presence of 425 mM external Na blocked (net) inward currents (noisy traces; 1.47 and 1.11 μA cm⁻², respectively). For illustration, a theoretical outward component of the observed net current was computed assuming an Ussing flux ratio exponent n′ = 1, and is shown (inverted) in each case as a smoother downward trace superimposed on the corresponding observed drop in ²²Na efflux.

Figure 2.

Recovery of inward current after removal of TTX. Axons were bathed in 425 mM Na seawater containing 0.2 μM TTX and internally dialyzed with 50 mM Na. Shortly after the bathing solution was replaced by one lacking TTX, the recovery of inward current became monoexponential. (A) Axon held at 0 mV. (B) A second axon held at −10 mV. Least-squares fits to the latter part of records A and B yielded exponential time constants of 3.19 ± 0.01 and 3.19 ± 0.02, respectively.

Figure 3.

Repeated (in alphabetical order) exposures to 0.2 μM TTX (each followed by ∼20 min of washout; not shown) of a single axon, bathed in 425 mM Na solution and internally dialyzed with Na-free solution, at various holding potentials. TTX reached the axon ∼40 s into each 5-min record. The leftmost column shows all the records made at −30 mV.

Figure 4.

Steady-state TTX-sensitive and background currents at various membrane potentials. (A) TTX-sensitive currents measured at −30 mV in records a, b, e, h, k, n, q, and t of Fig. 3 are plotted (closed circles) on a semi-log scale against the time after starting dialysis. Estimated values for TTX-sensitive current at −30 mV at the start of dialysis (closed triangle on the ordinate) and at the times measurements were made at other holding potentials (open circles) were obtained as described in the text. (B) Steady-state background current, measured at various holding potentials in the presence of TTX, is plotted against membrane voltage. The eight measurements made at −30 mV over 9 h are almost superimposed. (C) TTX-sensitive currents recorded at various holding potentials in Fig. 3 c, d, f, g, i, j, l, m, o, p, r, s, and u were scaled (to correct for rundown) to the reference values at −30 mV (from A) and plotted against holding potential (closed circles). The closed triangle at −30 mV is the normalization point. The theoretical curve is described in the text.

Figure 5.

Full and partial replacement of external Na by NMG, choline, or TMA. Axons were held at −30 mV and internally dialyzed with Na-free solution. Records were taken in alphabetical order. (A) Repeated exposure to 0.2 μM TTX in 425 mM Na (a, d, and g), choline (b), TMA (c), or NMG (e). (B) Same axon as in A; experiment continued (f–p) to include partial replacement of external Na by choline or TMA. (C) Repeated exposure to 0.2 μM TTX in solutions with [Na] between 425 and 0 mM (see column headings for Na mole fraction) replaced by equimolar NMG.

Figure 6.

Summary of external-Na substitution experiments like those shown in Fig. 5. Relative TTX-sensitive inward current is plotted against external [Na]. Replacement for Na was either choline (closed circles; 7 axons), TMA (open circles; 7 axons), or NMG (closed triangles; 10 axons). SEM not shown when smaller than the symbol. The dashed and solid lines are drawn according to Eqs. 1 and 2, respectively.

Figure 10.

Summary of the steady-state voltage dependence of normalized TTX-sensitive currents. (A) TTX-sensitive currents were measured at the Na concentrations indicated, given (in mM) as external [Na]/internal [Na]: 425/0 (nine axons; closed circles); 425/50 (nine axons; open circles); 266 (NMG replacement)/0 (nine axons; closed triangles); and 0 (choline replacement)/200 (seven axons; closed squares). Current amplitudes under all four conditions, at each membrane potential, were normalized to the current at −30 mV with 425 mM external Na and zero internal Na. The solid lines are calculated from a least-squares fit, to the entire dataset, of a permeation, steady-state gating, and (for the 266/0 condition) NMG block model described in discussion. The dashed line is described in the text. (B) Theoretical steady-state channel open probability functions p _a (Eq. 10) and p _ap_∞ (product of Eqs. 10 and 12), as described in discussion, calculated with the overall least-squares fit parameters listed in Table I.

Figure 7.

Reversal potential of the steady-state TTX-sensitive current. (A) An axon dialyzed with 184 mM Na and bathed in 111 mM Na (choline substitution) was repeatedly exposed to 0.2 μM TTX. Measurements were made at holding potentials of −30, 0, and −15 mV in the alphabetical sequence shown. (B) The TTX-sensitive current changes measured in A are plotted (closed circles) against the holding potential. The current change measured at −15 mV was not different from zero. The calculated equilibrium potential for Na (−12.7 mV) is shown as the open circle (E _Na). The solid line connecting the means at −30 and at 0 mV crosses the voltage axis at −14.4 mV.

Figure 9.

TTX-sensitive current with Na-free internal or external solution or with Na present on both sides. An axon held at −30 mV was initially dialyzed with Na-free (NMG) solution and bathed in 425 mM [Na]. After the response to 0.2 μM TTX was recorded (a), the dialysate was replaced by one containing 200 mM [Na] and the external medium by a Na-free, TTX-free solution (choline substitution). After another 30 min of dialysis, the response to 0.2 μM TTX was measured again (b). The external solution was then changed to TTX-free, 425 mM Na solution. After 30 min, the response to TTX was measured a third time (c). The record shown as c* was calculated from a, b, d, and e as described in the text. This protocol was repeated three more times in the same axon (records d–m), and a similar experiment with three repetitions of the protocol was done in another axon.