Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2002 Apr 30;99(9):6163-8.
doi: 10.1073/pnas.092576199.

Reverse engineering gene networks using singular value decomposition and robust regression

M K Stephen Yeung  1 , Jesper Tegnér, James J Collins
Affiliations

Reverse engineering gene networks using singular value decomposition and robust regression

M K Stephen Yeung et al. Proc Natl Acad Sci U S A. .

Abstract

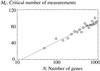
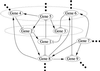
We propose a scheme to reverse-engineer gene networks on a genome-wide scale using a relatively small amount of gene expression data from microarray experiments. Our method is based on the empirical observation that such networks are typically large and sparse. It uses singular value decomposition to construct a family of candidate solutions and then uses robust regression to identify the solution with the smallest number of connections as the most likely solution. Our algorithm has O(log N) sampling complexity and O(N(4)) computational complexity. We test and validate our approach in a series of in numero experiments on model gene networks.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Number of errors, E, made by the reverse engineering scheme as a function of M, the number of measurements, for four linear networks of the form 1 with different sizes N.
Figure 2
Figure 2
Critical number of measurements, Mc, required to recover the entire connectivity matrix correctly, versus N, the size of the network for linear systems of the form 1. Circles: numerical data. Line: least-squares fit of the form Mc = a + b log N.
Figure 3
Figure 3
Number of errors, E, made by SVD alone (without the imposition of sparseness) as a function of M, the number of measurements, for four linear networks of the form 1 with different sizes N.
Figure 4
Figure 4
Schematic of a one-dimensional gene network with a cascade structure.
Figure 5
Figure 5
Number of errors, E, made by the reverse engineering scheme as a function of M, the number of measurements, for the repressing cascade 5 with N = 400 genes.
Figure 6
Figure 6
Schematic of a nonlinear gene network with a random structure.
Figure 7
Figure 7
Critical number of measurements, Mc, required to recover the entire connectivity matrix correctly, versus N, the size of the network for nonlinear systems of the form 7. Circles: numerical data. Line: least-squares fit of the form Mc = a + b log N.
Figure 8
Figure 8
Layer-by-layer recovery of network topology. Focusing on Gene 1, we can identify Genes 2 and 3 as the immediate upstream elements directly regulating Gene 1, and then Genes 4, 5, and 6 as next-immediate upstream elements indirectly regulating Gene 1.
See this image and copyright information in PMC

References

    1. Lockhart D J, Winzeler E A. Nature (London) 2000;405:827–836. - PubMed
    1. DeRisi J L, Iyer V R, Brown P O. Science. 1997;278:680–686. - PubMed
    1. Wen X, Fuhrman S, Michaels G S, Carr D B, Smith S, Barker J L, Somogyi R. Proc Natl Acad Sci USA. 1998;95:334–339. - PMC - PubMed
    1. Spellman P T, Sherlock G, Zhang M Q, Iyer V R, Anders K, Eisen M B, Brown P O, Botstein D, Futcher B. Mol Biol Cell. 1998;9:3273–3297. - PMC - PubMed
    1. Eisen M B, Spellman P T, Brown P O, Botstein D. Proc Natl Acad Sci USA. 1998;95:14863–14868. - PMC - PubMed

Publication types