The spatial dimensions of electrically coupled networks of interneurons in the neocortex
- PMID: 12019332
- PMCID: PMC6757663
- DOI: 10.1523/JNEUROSCI.22-10-04142.2002
The spatial dimensions of electrically coupled networks of interneurons in the neocortex
Abstract
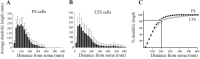
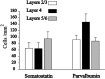
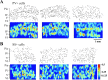
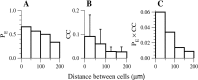
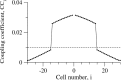
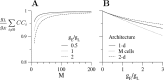
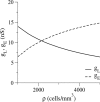
Inhibitory interneurons of the neocortex are electrically coupled to cells of the same type through gap junctions. We studied the spatial organization of two types of interneurons in the rat somatosensory cortex: fast-spiking (FS) parvalbumin-immunoreactive (PV+) cells, and low threshold-spiking (LTS) somatostatin-immunoreactive (SS+) cells. Paired recordings in layer 4 demonstrated that both the probability of coupling and the coupling coefficient drop steeply with intersomatic distance, reaching zero beyond 200 microm. The dendritic arbors of FS and LTS cells were reconstructed from electrophysiologically characterized, biocytin-filled cells; the two cell types had only minor differences in the number and span of their dendrites. However, there was a markedly higher density of PV+ cells than SS+ cells. PV+ cells were densest in layer 4, while SS+ cell density peaked in the subgranular layers. From these data we estimate that there is measurable electrical coupling (directly or indirectly via intermediary cells) between each interneuron and 20-50 others. The large number of electrical synapses implies that each interneuron participates in a large, continuous syncytium. To evaluate the functional significance of these findings, we examined several simple architectures of coupled networks analytically. We present a mathematical method to estimate the average summated coupling conductance that each cell receives from all of its neighbors, and the average leak conductance of individual cells, and we suggest that these have the same order of magnitude. These quantitative results have important implications for the effects of electrical coupling on the dynamic behavior of interneuron networks.
Figures
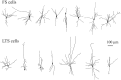


References
-
- Agmon A, Connors BW. Thalamocortical responses of mouse somatosensory (barrel) cortex in vitro. Neuroscience. 1991;41:365–379. - PubMed
-
- Akil M, Lewis DA. Differential distribution of parvalbumin-immunoreactive pericellular clusters of terminal boutons in developing and adult monkey neocortex. Exp Neurol. 1992;115:239–249. - PubMed
-
- Andreu E, Fernández E, Louis E, Ortega G, Sánchez-Andrés JV. Role of architecture in determining passive electrical properties in gap junction-connected cells. Pflügers Arch-Eur J Physiol. 2000;439:789–797. - PubMed
-
- Bayraktar T, Welker E, Freund TF, Zilles K, Staiger JF. Neurons immunoreactive for vasoactive intestinal polypeptide in the rat primary somatosensory cortex: morphology and spatial relationship to barrel-related columns. J Comp Neurol. 2000;420:291–304. - PubMed
-
- Beierlein M, Gibson JR, Connors BW. A network of electrically coupled interneurons drives synchronized inhibition in neocortex. Nat Neurosci. 2000;3:904–910. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
