Energy-efficient neuronal computation via quantal synaptic failures

Abstract

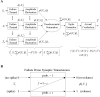
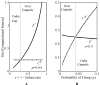
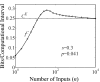
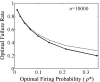
Organisms evolve as compromises, and many of these compromises can be expressed in terms of energy efficiency. For example, a compromise between rate of information processing and the energy consumed might explain certain neurophysiological and neuroanatomical observations (e.g., average firing frequency and number of neurons). Using this perspective reveals that the randomness injected into neural processing by the statistical uncertainty of synaptic transmission optimizes one kind of information processing relative to energy use. A critical hypothesis and insight is that neuronal information processing is appropriately measured, first, by considering dendrosomatic summation as a Shannon-type channel (1948) and, second, by considering such uncertain synaptic transmission as part of the dendrosomatic computation rather than as part of axonal information transmission. Using such a model of neural computation and matching the information gathered by dendritic summation to the axonal information transmitted, H(p*), conditions are defined that guarantee synaptic failures can improve the energetic efficiency of neurons. Further development provides a general expression relating optimal failure rate, f, to average firing rate, p*, and is consistent with physiologically observed values. The expression providing this relationship, f approximately 4(-H(p*)), generalizes across activity levels and is independent of the number of inputs to a neuron.

Fig. 1.

Partitioning communication and computation for a single neuron and its inputs. A, The presynaptic axonal inputs to the postsynaptic neuron is a multivariate binary vector, X = [X₁, X₂, …, X_n]. Each input, X_i, is subject to quantal failures, the result of which is denoted by φ (X_i), another binary vector that is then scaled by quantal amplitude, Q_i. Thus, each input provides excitation φ(X_i)Q_i. The dendrosomatic summation, ∑_iφ(X_i)Q_i is the endpoint of the computational process, and this sum is the input to the spike generator. Without specifying any particular subcellular locale, we absorb generic nonlinearities that precede the spike generator into the spike generator, g (∑_iφ(X_i)Q_i). The spike generator output is a binary variable, Z, which is faithfully transmitted down the axon as Z′. ThisZ′ is just another X_i elsewhere in the network. In neocortex, experimental evidence indicates that axonal conduction is, essentially, information lossless, as a resultI(Z; Z′) ≈ H(Z). The information transmitted through synapses and dendrosomatic summation is measured by the mutual information I(X; ∑ φ(X_i)Q_i) = H(X) − H(X‖∑_iφ(X_i)Q_i). Given the assumptions in the text combined with one of Shannon's source-channel theorems implies that, H(X) − H(X‖∑_iφ(X_i)Q_i) = H(p*), where H(p*) is the energy-efficient maximum value of H(Z). B, The model of failure prone synaptic transmission. An input value of 0, i.e., no spike, always yields an output value of 0, i.e., no transmitter release. An input value of 1, an axonal spike, produces an output value of 1, transmitter release, with probability success s = 1 − f. A failure occurs when an input value of 1 produces an output value of 0. The probability of failure is denoted by f.

Fig. 2.

A, The optimal failure rate (1 − s) of theorem G and corollary F is obtained by noting the intersection of the two curves, I^C (the computational information) and C^E = H(p*) (the output channel capacity). At higher values of s, any input information greater than H(p*) that survives the input-based computational process of summation is wasted because the information rate out cannot exceed H(p*), the output axonal energy-efficient channel capacity. These values define an overcapacity region. For lower values of s, neuronal integration is unable to provide enough information to the spike generator to fully use the available rate of the axon. This is the undercapacity region. Of course, changing p* changes the optimal failure rate because the C^E curve will shift. These curves also reveal that a slight relaxation of assumption A4 will not change the intersection value of s very much (e.g., a 10% information loss at the spike generator produces a <3% change in the value of s). The success rate s equals one minus the failure rate. The optimal success rate is demarcated by thevertical dotted line. In this figure the output channel capacity, H(p*), uses p* = 0.041; n = 10,000 inputs. B , An alternative perspective. Assuming the failure rate is given as 0.7 by physiological measurements, then we could determine p*, the p that matches computational information I^C to the energy-efficient channel capacity. Again the vertical dotted line indicates the predicted value; n = 10,000. Both A and B are calculated using the binomial probabilities of the .

Fig. 3.

At the optimal failure rate, matching I^C to C^E is increasingly robust as number of inputs, n, increases. Nevertheless I^C, the mutual information measure of computation, attains the approximate value of output capacity, C^E, for n as small as 200. Calculations used the binomial distributions of the with failure rate fixed at 0.7 and p* set to 0.041. Thedashed line indicates H(p*).

Fig. 4.

Optimal failure rate as a function of spike probability in one computational interval. The optimal failure rate decreases monotonically as firing probability increases so that this theory accommodates a wide range of firing levels. The vicinity of physiological p* (0.025–0.05 for nonmotor neocortex and limbic cortex) predicts physiologically observed failure rates. Thedashed line plots f = (1/4)^H(p*), whereas the solid line is calculated without the Gaussian approximations described in the. Note the good quality of the approximation in the region of interest (p* ≈ .05), although for very active neurons the approximation will overestimate the optimal failure rate. More important than this small approximation error, we would still restrict this theory to places where information theoretic principles, as opposed to decision theoretic or control theoretic principles, best characterize information processing.