Three-dimensional image reconstructions of the contractile tail of T4 bacteriophage
- PMID: 1206701
- PMCID: PMC3920174
- DOI: 10.1016/s0022-2836(75)80158-6
Three-dimensional image reconstructions of the contractile tail of T4 bacteriophage
Abstract
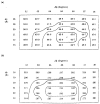
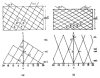
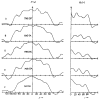
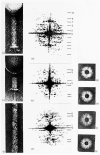
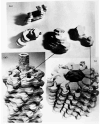
The three-dimensional structures of the extended T4 phage tail and polysheath, an aberrant form of the contracted tail sheath, have both been reconstructed from electron micrographs. The reconstructed map of the extended structure is at a somewhat higher resolution (~20 Å) than an earlier reconstruction, allowing tentative boundaries to be drawn between the individual protein subunits in the tail sheath. This improvement has been achieved by testing the degree of correlation between data from different images as part of the selection procedure and averaging the most highly correlated sets of data. Details of the correlation are given in the Appendix. The resolution of the map of the contracted structure is lower than that of the extended tail, in spite of a similar averaging of several images, because of the higher degree of distortion in this structure. Nevertheless, it has been possible, to some extent, to trace the changes in conformation of the subunit during contraction.
Figures


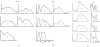





References
-
- Amos LA, Klug A. J. Cell Sci. 1974;14:523–549. - PubMed
-
- Arndt UW, Crowther RA, Mallett JFW. J. Scient. Instrum. 1968;1:510–516. - PubMed
-
- Bayer ME, Remsen CC. Virology. 1970;40:703–718. - PubMed
-
- Crowther RA. Phil. Trans. Roy. Soc. London. 1971;261:221–230. - PubMed
-
- Crowther RA, Amos LA. J. Mol. Biol. 1971;60:123–130. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

