Fast-folding protein kinetics, hidden intermediates, and the sequential stabilization model

Abstract

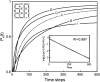
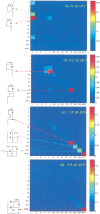
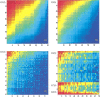
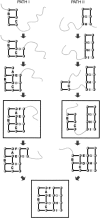
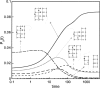
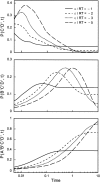
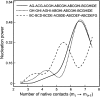
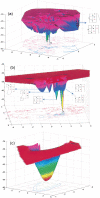
Do two-state proteins fold by pathways or funnels? Native-state hydrogen exchange experiments show discrete nonnative structures in equilibrium with the native state. These could be called hidden intermediates (HI) because their populations are small at equilibrium, and they are not detected in kinetic experiments. HIs have been invoked as disproof of funnel models, because funnel pictures appear to indicate (1) no specific sequences of events in folding; (2) a continuum, rather than a discrete ladder, of structures; and (3) smooth landscapes. In the present study, we solve the exact dynamics of a simple model. We find, instead, that the present microscopic model is indeed consistent with HIs and transition states, but such states occur in parallel, rather than along the single pathway predicted by the sequential stabilization model. At the microscopic level, we observe a huge multiplicity of trajectories. But at the macroscopic level, we observe two pathways of specific sequences of events that are relatively traditional except that they are in parallel, so there is not a single reaction coordinate. Using singular value decomposition, we show an accurate representation of the shapes of the model energy landscapes. They are highly complex funnels.

Fig. 1.

Time evolution of native contacts for the 16-mer. The time-dependent probability P_X(t) of contacts X = A–D, G, I is shown. The inset shows the plot of ln{[P_N(t) − P_N(∞)]/[P_N(0) − P_N(∞)]} versus time where P_N(t) is the probability of native state. The close fit (correlation coefficient = 0.997) to a line shows that the observed kinetics is single exponential.

Fig. 2.

Joint probabilities P(X, t₁; Y, t₂) of macroconformation X (abscissa) at time t₁ and macroconformation Y (ordinate) at time t₂, calculated for various time intervals t₁ ≤ t ≤ t₂. See the color code on the right bar for the range of the probability values. The macroconformations stabilized at different stages are explicitly displayed on the left margin, along with their instantaneous probabilities.

Fig. 3.

Transition rates C (m + 1|m) between macroconformations having m (abscissa) and m + 1 (ordinate) native contacts, for m = 2, 3, and 4, shown in the maps (a–c). Map d shows the transitions to macroconformations with 7, 8, and finally 9 (all) contacts, starting from m = 5. Macroconformations are assigned serial indices in the order of decreasing conformational entropies (see Table 2). The color code, red-orange-yellow-green-cyan-blue, refers to decreasing transition probabilities. The uniform shading in a and b indicates the strong correlation between transition probabilities and conformational entropies. The spots in c signal the interference of specific interactions, which become more pronounced in d.

Fig. 4.

Two parallel macropaths I and II observed in the folding kinetics of the investigated 16-mer. The macropath I on the left is the fastest macropath and dominates the macroscopic folding rate.

Fig. 5.

Time evolution of substructured 16-mer macroconformations. The peaks observed indicate the tendencies to accumulate before complete folding.

Fig. 6.

(a) Folding profile for apparent two-state folding proteins, composed of an initial rate-limiting barrier (TS) succeeded by sequentially stabilized intermediates, proposed by Englander and coworkers (Englander and Kallenbach 1983;Rumbley et al. 2001). (b) Time evolution of the probability of the states U, I₁, I₂ and N for the sequential scheme U〉I₁〉I₂〉N, using the rate constants 10⁻²,10⁻⁴, and 10⁻⁶/unit time for the respective steps U>I₁, I₁〉I₂, and I₂〉N, and the initial conditions P_U(0) = 1 and P_I1(0) = P_I2(0) = P_N(0) = 0.

Fig. 6.

(a) Folding profile for apparent two-state folding proteins, composed of an initial rate-limiting barrier (TS) succeeded by sequentially stabilized intermediates, proposed by Englander and coworkers (Englander and Kallenbach 1983;Rumbley et al. 2001). (b) Time evolution of the probability of the states U, I₁, I₂ and N for the sequential scheme U〉I₁〉I₂〉N, using the rate constants 10⁻²,10⁻⁴, and 10⁻⁶/unit time for the respective steps U>I₁, I₁〉I₂, and I₂〉N, and the initial conditions P_U(0) = 1 and P_I1(0) = P_I2(0) = P_N(0) = 0.

Fig. 7.

Time evolution of the partially folded substructures B‘C‘ and B‘C‘D‘, and native structure A‘B‘C‘D‘, for the 9-mer displayed in Table 1a, calculated for the indicated ɛ/kT ratios. The accumulation of the intermediates is diminished at higher temperatures (or weaker intramolecular interactions).

Fig. 8.

Nucleation power of native contacts along particular macroroutes, indicated by the incremental change in folding time τ_m succeeding the formation of each contact m, relative to the overall folding time τ₀. The ratio Δτ/τ₀ = (τ_m−1 − τ_m)/τ₀ is shown for each passage from m − 1 to m contacts along four different macroroutes.

Fig. 9.

Energy landscape obtained by projecting the conformations onto the two-dimensional normal space found by the singular value decomposition of the 32-dimensional vectors defining the individual conformations. Parts a, b, and c refer to subsets of conformations having more than m = 4, 5, and 6 native contacts, respectively. The native conformation is labeled as N.