Supply-demand balance and metabolic scaling
- PMID: 12149461
- PMCID: PMC124956
- DOI: 10.1073/pnas.162216899
Supply-demand balance and metabolic scaling
Abstract
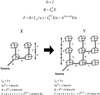
It is widely accepted that metabolic rates scale across species approximately as the 3/4 power of mass in most if not all groups of organisms. Metabolic demand per unit mass thus decreases as body mass increases. Metabolic rates reflect both the ability of the organism's transport system to deliver metabolites to the tissues and the rate at which the tissues use them. We show that the ubiquitous 3/4 power law for interspecific metabolic scaling arises from simple, general geometric properties of transportation networks constrained to function in biological organisms. The 3/4 exponent and other observed scaling relationships follow when mass-specific metabolic demands match the changing delivery capacities of the network at different body sizes. Deviation from the 3/4 exponent suggests either inefficiency or compensating physiological mechanisms. Our conclusions are based on general arguments incorporating the minimum of biological detail and should therefore apply to the widest range of organisms.
Figures
Comment in
-
Comment on "Revising the distributive networks models of West, Brown and Enquist (1997) and Banavar, Maritan and Rinaldo (1999): Metabolic inequity of living tissues provides clues for the observed allometric scaling rules" by Makarieva, Gorshkov and Li.J Theor Biol. 2006 Apr 7;239(3):391-3. doi: 10.1016/j.jtbi.2005.08.023. Epub 2005 Sep 28. J Theor Biol. 2006. PMID: 16197962 No abstract available.
Similar articles
-
Reconciling theories for metabolic scaling.J Anim Ecol. 2014 Jan;83(1):20-9. doi: 10.1111/1365-2656.12085. Epub 2013 May 13. J Anim Ecol. 2014. PMID: 23668377
-
Ontogenetic and interspecific metabolic scaling in insects.Am Nat. 2014 Dec;184(6):695-701. doi: 10.1086/678401. Epub 2014 Oct 28. Am Nat. 2014. PMID: 25438170
-
Shape shifting predicts ontogenetic changes in metabolic scaling in diverse aquatic invertebrates.Proc Biol Sci. 2015 Mar 7;282(1802):20142302. doi: 10.1098/rspb.2014.2302. Proc Biol Sci. 2015. PMID: 25652833 Free PMC article.
-
A unifying explanation for diverse metabolic scaling in animals and plants.Biol Rev Camb Philos Soc. 2010 Feb;85(1):111-38. doi: 10.1111/j.1469-185X.2009.00095.x. Epub 2009 Nov 6. Biol Rev Camb Philos Soc. 2010. PMID: 19895606 Review.
-
Analytic theories of allometric scaling.J Exp Biol. 2011 Apr 1;214(Pt 7):1055-62. doi: 10.1242/jeb.054502. J Exp Biol. 2011. PMID: 21389188 Review.
Cited by
-
Modeling nitrogen flux by larval insect herbivores from a temperate hardwood forest.Oecologia. 2007 Oct;153(4):833-43. doi: 10.1007/s00442-007-0797-9. Epub 2007 Jul 18. Oecologia. 2007. PMID: 17636338
-
Exploring network scaling through variations on optimal channel networks.Proc Natl Acad Sci U S A. 2013 Nov 26;110(48):19295-300. doi: 10.1073/pnas.1313866110. Epub 2013 Nov 11. Proc Natl Acad Sci U S A. 2013. PMID: 24218573 Free PMC article.
-
Sociohydrology: Scientific Challenges in Addressing the Sustainable Development Goals.Water Resour Res. 2019 Aug;55(8):6327-6355. doi: 10.1029/2018WR023901. Epub 2019 Aug 16. Water Resour Res. 2019. PMID: 32742038 Free PMC article.
-
Allometric Scaling of Clearance in Paediatric Patients: When Does the Magic of 0.75 Fade?Clin Pharmacokinet. 2017 Mar;56(3):273-285. doi: 10.1007/s40262-016-0436-x. Clin Pharmacokinet. 2017. PMID: 27510367 Free PMC article.
-
The scaling and temperature dependence of vertebrate metabolism.Biol Lett. 2006 Mar 22;2(1):125-7. doi: 10.1098/rsbl.2005.0378. Biol Lett. 2006. PMID: 17148344 Free PMC article.
References
-
- McMahon T. A. & Bonner, J. T., (1983) On Size and Life (Freeman, New York).
-
- Bonner J. T., (1983) The Evolution of Complexity by Means of Natural Selection (Princeton Univ. Press, Princeton).
-
- Peters R. H., (1983) The Ecological Implications of Body Size (Cambridge Univ. Press, Cambridge, U.K.).
-
- Schmidt-Nielsen K., (1984) Scaling: Why Is Animal Size So Important? (Cambridge Univ. Press, Cambridge, U.K.).
-
- Calder W. A., (1984) Size, Function, and Life History (Harvard Univ. Press, Cambridge, MA).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

