The transitive fallacy for randomized trials: if A bests B and B bests C in separate trials, is A better than C?
- PMID: 12429069
- PMCID: PMC137603
- DOI: 10.1186/1471-2288-2-13
The transitive fallacy for randomized trials: if A bests B and B bests C in separate trials, is A better than C?
Erratum in
- BMC Med Res Methodol. 2003 Oct 29;3(1):23
Abstract
Background: If intervention A bests B in one randomized trial, and B bests C in another randomized trial, can one conclude that A is better than C? The problem was motivated by the planning of a randomized trial, where A is spiral-CT screening, B is x-ray screening, and C is no screening. On its surface, this would appear to be a straightforward application of the transitive principle of logic.
Methods: We extended the graphical approach for omitted binary variables that was originally developed to illustrate Simpson's paradox, applying it to hypothetical, but plausible scenarios involving lung cancer screening, treatment for gastric cancer, and antibiotic therapy for clinical pneumonia.
Results: Graphical illustrations of the three examples show different ways the transitive fallacy for randomized trials can arise due to changes in an unobserved or unadjusted binary variable. In the most dramatic scenario, B bests C in the first trial, A bests B in the second trial, but C bests A at the time of the second trial.
Conclusion: Even with large sample sizes, combining results from a previous randomized trial of B versus C with results from a new randomized trial of A versus B will not guarantee correct inference about A versus C. A three-arm trial of A, B, and C would protect against this problem and should be considered when the sequential trials are performed in the context of changing secular trends in important omitted variables such as therapy in cancer screening trials.
Figures


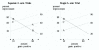
References
-
- Langford E, Schwertman N, Owens M. Is the property of being positively correlated transitive? The American Statistician. 2001;55:322–325. doi: 10.1198/000313001753272286. - DOI
-
- Paulos JA. I Think Therefore I Laugh: The Flip Side of Philosophy. New York: Columbia University Press. 2000. pp. 23–29.
-
- Wainer H. The BK-Plot: Making Simpson's paradox clear to the masses, Chance. pp. 60–62.
-
- Fontana RS, Sanderson DR, Woolner LB, Taylor WF, Miller WE, Muhm JR, et al. Screening for lung cancer: a critique of the Mayo Lung Project. Cancer. 1991;67:1155–64. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources

