The role of chromosomal instability in tumor initiation

Abstract

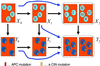
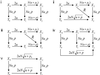
Chromosomal instability (CIN) is a defining characteristic of most human cancers. Mutation of CIN genes increases the probability that whole chromosomes or large fractions of chromosomes are gained or lost during cell division. The consequence of CIN is an imbalance in the number of chromosomes per cell (aneuploidy) and an enhanced rate of loss of heterozygosity. A major question of cancer genetics is to what extent CIN, or any genetic instability, is an early event and consequently a driving force for tumor progression. In this article, we develop a mathematical framework for studying the effect of CIN on the somatic evolution of cancer. Specifically, we calculate the conditions for CIN to initiate the process of colorectal tumorigenesis before the inactivation of tumor suppressor genes.

Fig 1.

Mutational network of cancer initiation describing inactivation of a TSP gene and activation of CIN. Normal cells, x₀, have two functioning copies of the gene and no CIN. Cells with one inactivated copy, x₁, arise from x₀ cells at a rate of 2u; each copy can mutate with probability u per cell division. Cells with two inactivated copies of the TSP gene, x₂, arise from x₁ cells at a rate of u + p₀. The parameter p₀ describes the probability that the second copy of the TSP gene is lost during a cell division because of LOH. CIN cells, y_i, arise from non-CIN cells, x_i, at a rate of u_c = 2n_cu, where n_c denotes the number of genes that cause CIN if a single copy of them is mutated or inactivated. CIN cells with two functioning copies of the TSP gene, y₀, mutate into y₁ cells at a rate of 2u. CIN cells of type y₁ mutate to y₂ cells at a rate of u + p, where p is the rate of LOH in CIN cells. We expect p to be much greater than u and p₀. For simplicity, we neglect the possibility that APC might be inactivated by an LOH event followed by a point mutation. If CIN (or LOH in 5q) has a cost, then this pathway will contribute very little; otherwise it could enhance the relative success of CIN by a factor of ≈2.

Fig 2.

The early steps of colon cancer occur in small crypts that contain a few thousand cells. The whole crypt is replenished from a small number of stem cells. The effective population size of the crypt, N, with respect to the somatic evolution of cancer might be of the order of 10 cells. As long as N² ≪ 1/u (where u ≈ 10⁻⁷–10⁻⁶), then there is a high probability that at any one time crypts contain cells of only one type. Hence, we can investigate a stochastic process describing transitions among six different states, X₀, X₁, X₂, Y₀, Y₁, and Y₂, referring to homogeneous crypts of cell type x₀, x₁, x₂, y₀, y₁, and y₂, respectively. The transitions reflect the mutational network of Fig. 1. In addition, there are three stochastic tunnels. For certain parameter values, the system can tunnel from X₀ to X₂ without reaching X₁. Similarly, there are tunnels from Y₀ to Y₂ and from X₁ to Y₂. Tunnels occur if the second step in a consecutive transition is much faster than the first one and if the final cell has a strong selective advantage.

Fig 3.

Transition rates and stochastic tunnels of the probabilistic process describing the dynamics of early steps in colon cancer. The states X₀, X₁, and X₂ refer to homogeneous crypts of non-CIN cells with 0, 1, and 2 inactivated copies of APC, respectively. The states Y₀, Y₁, and Y₂ refer to homogeneous crypts of CIN cells with 0, 1, and 2 inactivated copies of APC, respectively. The probability that a CIN cell with reproductive rate r reaches fixation in a crypt of N cells is given by ρ = r^N−1(1 − r)/(1 − r^N). The mutation rate per gene per cell division is given by u. The mutation rate from non-CIN cells to CIN cells is given by u_c = 2n_cu, where n_c is the number of genes that cause CIN if one copy of them is mutated. The rate of LOH in CIN and non-CIN cells is given by p and p₀, respectively. Let γ = (1 − r)²r^N−2 if r < 1 and γ = (r − 1)/{rN log[N(r − 1)/r]} if r > 1. Network i occurs in two cases: (ia) ≪ 1/N and |1 − r| ≪ 1/N and (ib) ≪ 1/N and |1 − r| ≫ 1/N and p ≪ γ. Network ii occurs in three cases: (iia) if ≫ 1/N and |1 − r| ≪ , then R = Nu_c, (iib) if r < 1 and ≫ 1/N and 1 − r ≫ , then R = Nu_cpr/(1 − r), and (iic) if r > 1 and ≫ 1/N and r − 1 ≫ and p ≫ γ, then R = N²u_cplog[N(r − 1)/r]. Network iii occurs if r < 1, p ≫ γ, and ≪ 1/N ≪ 1 − r; we have R = Nu_cpr/(1 − r). Network iv occurs if r > 1, p ≪ γ, and r − 1 ≫ ≫ 1/N. In addition, networks i–iv require that ≪ 1/N. Network v occurs if ≫ 1/N. This is a complete classification of all generic cases.