Fine gating properties of channels responsible for persistent sodium current generation in entorhinal cortex neurons
- PMID: 12451054
- PMCID: PMC2229567
- DOI: 10.1085/jgp.20028676
Fine gating properties of channels responsible for persistent sodium current generation in entorhinal cortex neurons
Abstract
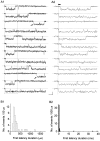
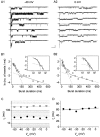
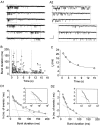
The gating properties of channels responsible for the generation of persistent Na(+) current (I(NaP)) in entorhinal cortex layer II principal neurons were investigated by performing cell-attached, patch-clamp experiments in acutely isolated cells. Voltage-gated Na(+)-channel activity was routinely elicited by applying 500-ms depolarizing test pulses positive to -60 mV from a holding potential of -100 mV. The channel activity underlying I(NaP) consisted of prolonged and frequently delayed bursts during which repetitive openings were separated by short closings. The mean duration of openings within bursts was strongly voltage dependent, and increased by e times per every approximately 12 mV of depolarization. On the other hand, intraburst closed times showed no major voltage dependence. The mean duration of burst events was also relatively voltage insensitive. The analysis of burst-duration frequency distribution returned two major, relatively voltage-independent time constants of approximately 28 and approximately 190 ms. The probability of burst openings to occur also appeared largely voltage independent. Because of the above "persistent" Na(+)-channel properties, the voltage dependence of the conductance underlying whole-cell I(NaP) turned out to be largely the consequence of the pronounced voltage dependence of intraburst open times. On the other hand, some kinetic properties of the macroscopic I(NaP), and in particular the fast and intermediate I(NaP)-decay components observed during step depolarizations, were found to largely reflect mean burst duration of the underlying channel openings. A further I(NaP) decay process, namely slow inactivation, was paralleled instead by a progressive increase of interburst closed times during the application of long-lasting (i.e., 20 s) depolarizing pulses. In addition, long-lasting depolarizations also promoted a channel gating modality characterized by shorter burst durations than normally seen using 500-ms test pulses, with a predominant burst-duration time constant of approximately 5-6 ms. The above data, therefore, provide a detailed picture of the single-channel bases of I(NaP) voltage-dependent and kinetic properties in entorhinal cortex layer II neurons.
Figures




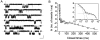



Similar articles
-
Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons: a whole-cell and single-channel study.J Gen Physiol. 1999 Oct;114(4):491-509. doi: 10.1085/jgp.114.4.491. J Gen Physiol. 1999. PMID: 10498669 Free PMC article.
-
High conductance sustained single-channel activity responsible for the low-threshold persistent Na(+) current in entorhinal cortex neurons.J Neurosci. 1999 Sep 1;19(17):7334-41. doi: 10.1523/JNEUROSCI.19-17-07334.1999. J Neurosci. 1999. PMID: 10460240 Free PMC article.
-
Kinetic diversity of single-channel burst openings underlying persistent Na(+) current in entorhinal cortex neurons.Biophys J. 2003 Nov;85(5):3019-34. doi: 10.1016/S0006-3495(03)74721-3. Biophys J. 2003. PMID: 14581203 Free PMC article.
-
Multiple conductance substates in pharmacologically untreated Na(+) channels generating persistent openings in rat entorhinal cortex neurons.J Membr Biol. 2006;214(3):165-80. doi: 10.1007/s00232-006-0068-4. Epub 2007 Jun 8. J Membr Biol. 2006. PMID: 17558531
-
Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex.J Neurosci. 1993 Feb;13(2):660-73. doi: 10.1523/JNEUROSCI.13-02-00660.1993. J Neurosci. 1993. PMID: 8381170 Free PMC article.
Cited by
-
Kinetic and functional analysis of transient, persistent and resurgent sodium currents in rat cerebellar granule cells in situ: an electrophysiological and modelling study.J Physiol. 2006 May 15;573(Pt 1):83-106. doi: 10.1113/jphysiol.2006.106682. Epub 2006 Mar 9. J Physiol. 2006. PMID: 16527854 Free PMC article.
-
Realistic modeling of entorhinal cortex field potentials and interpretation of epileptic activity in the guinea pig isolated brain preparation.J Neurophysiol. 2006 Jul;96(1):363-77. doi: 10.1152/jn.01342.2005. Epub 2006 Apr 5. J Neurophysiol. 2006. PMID: 16598061 Free PMC article.
-
Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing.J Neurosci. 2010 Oct 13;30(41):13850-60. doi: 10.1523/JNEUROSCI.0547-10.2010. J Neurosci. 2010. PMID: 20943925 Free PMC article.
-
Spontaneous activity of dopaminergic retinal neurons.Biophys J. 2003 Oct;85(4):2158-69. doi: 10.1016/S0006-3495(03)74642-6. Biophys J. 2003. PMID: 14507682 Free PMC article.
-
Cortical neurons derived from human pluripotent stem cells lacking FMRP display altered spontaneous firing patterns.Mol Autism. 2020 Jun 19;11(1):52. doi: 10.1186/s13229-020-00351-4. Mol Autism. 2020. PMID: 32560741 Free PMC article.
References
-
- Agrawal, N., B.M. Hamam, J. Magistretti, A. Alonso, and D.S. Ragsdale. 2001. Persistent sodium channel activity mediates subthreshold membrane potential oscillations and low-threshold spikes in entorhinal cortex layer V neurons. Neuroscience. 102:53–64. - PubMed
-
- Aldrich, R.W., D.P. Corey, and C.F. Stevens. 1983. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature. 306:436–441. - PubMed
-
- Alonso, A., and E. García-Austt. 1987. a. Neuronal sources of theta rhythm in the entorhinal cortex of the rat. I. Laminar distribution of theta field potentials. Exp. Brain Res. 67:493–501. - PubMed
-
- Alonso, A., and E. García-Austt. 1987. b. Neuronal sources of theta rhythm in the entorhinal cortex of the rat. II. Phase relations between unit discharges and theta field potentials. Exp. Brain Res. 67:502–509. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

