Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells
- PMID: 12482886
- PMCID: PMC2290731
- DOI: 10.1113/jphysiol.2002.029249
Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells
Abstract
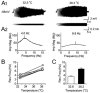
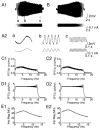
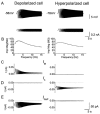
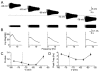
Coherent network oscillations in the brain are correlated with different behavioural states. Intrinsic resonance properties of neurons provide a basis for such oscillations. In the hippocampus, CA1 pyramidal neurons show resonance at theta (theta) frequencies (2-7 Hz). To study the mechanisms underlying theta-resonance, we performed whole-cell recordings from CA1 pyramidal cells (n = 73) in rat hippocampal slices. Oscillating current injections at different frequencies (ZAP protocol), revealed clear resonance with peak impedance at 2-5 Hz at approximately 33 degrees C (increasing to approximately 7 Hz at approximately 38 degrees C). The theta-resonance showed a U-shaped voltage dependence, being strong at subthreshold, depolarized (approximately -60 mV) and hyperpolarized (approximately -80 mV) potentials, but weaker near the resting potential (-72 mV). Voltage clamp experiments revealed three non-inactivating currents operating in the subthreshold voltage range: (1) M-current (I(M)), which activated positive to -65 mV and was blocked by the M/KCNQ channel blocker XE991 (10 microM); (2) h-current (I(h)), which activated negative to -65 mV and was blocked by the h/HCN channel blocker ZD7288 (10 microM); and (3) a persistent Na(+) current (I(NaP)), which activated positive to -65 mV and was blocked by tetrodotoxin (TTX, 1 microM). In current clamp, XE991 or TTX suppressed the resonance at depolarized, but not hyperpolarized membrane potentials, whereas ZD7288 abolished the resonance only at hyperpolarized potentials. We conclude that these cells show two forms of theta-resonance: "M-resonance" generated by the M-current and persistent Na(+) current in depolarized cells, and "H-resonance" generated by the h-current in hyperpolarized cells. Computer simulations supported this interpretation. These results suggest a novel function for M/KCNQ channels in the brain: to facilitate neuronal resonance and network oscillations in cortical neurons, thus providing a basis for an oscillation-based neural code.
Figures







Similar articles
-
Theta-frequency membrane resonance and its ionic mechanisms in rat subicular pyramidal neurons.Neuroscience. 2006 Jun 19;140(1):45-55. doi: 10.1016/j.neuroscience.2006.01.033. Epub 2006 Mar 9. Neuroscience. 2006. PMID: 16527421
-
Subthreshold membrane resonance in neocortical neurons.J Neurophysiol. 1996 Aug;76(2):683-97. doi: 10.1152/jn.1996.76.2.683. J Neurophysiol. 1996. PMID: 8871191
-
SK- and h-current contribute to the generation of theta-like resonance of rat substantia nigra pars compacta dopaminergic neurons at hyperpolarized membrane potentials.Brain Struct Funct. 2012 Apr;217(2):379-94. doi: 10.1007/s00429-011-0361-6. Epub 2011 Nov 23. Brain Struct Funct. 2012. PMID: 22108680
-
Kv7/KCNQ/M and HCN/h, but not KCa2/SK channels, contribute to the somatic medium after-hyperpolarization and excitability control in CA1 hippocampal pyramidal cells.J Physiol. 2005 Aug 1;566(Pt 3):689-715. doi: 10.1113/jphysiol.2005.086835. Epub 2005 May 12. J Physiol. 2005. PMID: 15890705 Free PMC article.
-
Intrinsic theta-frequency membrane potential oscillations in hippocampal CA1 interneurons of stratum lacunosum-moleculare.J Neurophysiol. 1999 Mar;81(3):1296-307. doi: 10.1152/jn.1999.81.3.1296. J Neurophysiol. 1999. PMID: 10085356
Cited by
-
Postnatal development of electrophysiological properties of principal neurons in the rat basolateral amygdala.J Physiol. 2012 Oct 1;590(19):4819-38. doi: 10.1113/jphysiol.2012.237453. Epub 2012 Jul 30. J Physiol. 2012. PMID: 22848043 Free PMC article.
-
Effects of Ih and TASK-like shunting current on dendritic impedance in layer 5 pyramidal-tract neurons.J Neurophysiol. 2021 Apr 1;125(4):1501-1516. doi: 10.1152/jn.00015.2021. Epub 2021 Mar 10. J Neurophysiol. 2021. PMID: 33689489 Free PMC article.
-
Kv7/KCNQ channels control action potential phasing of pyramidal neurons during hippocampal gamma oscillations in vitro.J Neurosci. 2009 Oct 21;29(42):13353-64. doi: 10.1523/JNEUROSCI.1463-09.2009. J Neurosci. 2009. PMID: 19846723 Free PMC article.
-
Somatodendritic Kv7/KCNQ/M channels control interspike interval in hippocampal interneurons.J Neurosci. 2006 Nov 22;26(47):12325-38. doi: 10.1523/JNEUROSCI.3521-06.2006. J Neurosci. 2006. PMID: 17122058 Free PMC article.
-
Double Trouble? Potential for Hyperexcitability Following Both Channelopathic up- and Downregulation of I(h) in Epilepsy.Front Neurosci. 2009 May 1;3(1):25-33. doi: 10.3389/neuro.01.005.2009. eCollection 2009 May. Front Neurosci. 2009. PMID: 19753094 Free PMC article.
References
-
- Alonso A, Klink R. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. Journal of Neurophysiology. 1993;70:128–143. - PubMed
-
- Alonso A, Llinas RR. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 1989;342:175–177. - PubMed
-
- Bland BH. The physiology and pharmacology of hippocampal formation theta rhythms. Progress in Neurobiology. 1986;26:1–54. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

