Isolation of relevant visual features from random stimuli for cortical complex cells
- PMID: 12486174
- PMCID: PMC6758424
- DOI: 10.1523/JNEUROSCI.22-24-10811.2002
Isolation of relevant visual features from random stimuli for cortical complex cells
Abstract
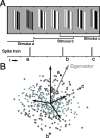
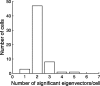
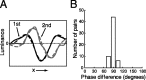
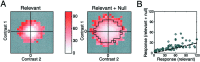
A crucial step in understanding the function of a neural circuit in visual processing is to know what stimulus features are represented in the spiking activity of the neurons. For neurons with complex, nonlinear response properties, characterization of feature representation requires measurement of their responses to a large ensemble of visual stimuli and an analysis technique that allows identification of relevant features in the stimuli. In the present study, we recorded the responses of complex cells in the primary visual cortex of the cat to spatiotemporal random-bar stimuli and applied spike-triggered correlation analysis of the stimulus ensemble. For each complex cell, we were able to isolate a small number of relevant features from a large number of null features in the random-bar stimuli. Using these features as visual stimuli, we found that each relevant feature excited the neuron effectively in isolation and contributed to the response additively when combined with other features. In contrast, the null features evoked little or no response in isolation and divisively suppressed the responses to relevant features. Thus, for each cortical complex cell, visual inputs can be decomposed into two distinct types of features (relevant and null), and additive and divisive interactions between these features may constitute the basic operations in visual cortical processing.
Figures



Similar articles
-
Computational subunits of visual cortical neurons revealed by artificial neural networks.Proc Natl Acad Sci U S A. 2002 Jun 25;99(13):8974-9. doi: 10.1073/pnas.122173799. Epub 2002 Jun 11. Proc Natl Acad Sci U S A. 2002. PMID: 12060706 Free PMC article.
-
Stimulus-dependent oscillations in the cat visual cortex: differences between bar and grating stimuli.Brain Res. 1996 Aug 26;731(1-2):91-100. doi: 10.1016/0006-8993(96)00468-4. Brain Res. 1996. PMID: 8883858
-
Direction selectivity of synaptic potentials in simple cells of the cat visual cortex.J Neurophysiol. 1997 Nov;78(5):2772-89. doi: 10.1152/jn.1997.78.5.2772. J Neurophysiol. 1997. PMID: 9356425
-
Processing of complex stimuli and natural scenes in the visual cortex.Curr Opin Neurobiol. 2004 Aug;14(4):468-73. doi: 10.1016/j.conb.2004.06.002. Curr Opin Neurobiol. 2004. PMID: 15302353 Review.
-
The dynamics of visual responses in the primary visual cortex.Prog Brain Res. 2007;165:21-32. doi: 10.1016/S0079-6123(06)65003-6. Prog Brain Res. 2007. PMID: 17925238 Review.
Cited by
-
The role of delayed suppression in slow and fast contrast adaptation in V1 simple cells.J Neurosci. 2013 Apr 10;33(15):6388-400. doi: 10.1523/JNEUROSCI.3609-12.2013. J Neurosci. 2013. PMID: 23575837 Free PMC article.
-
Receptive field properties of neurons in the early visual cortex revealed by local spectral reverse correlation.J Neurosci. 2006 Mar 22;26(12):3269-80. doi: 10.1523/JNEUROSCI.4558-05.2006. J Neurosci. 2006. PMID: 16554477 Free PMC article.
-
Coding of chromatic spatial contrast by macaque V1 neurons.Elife. 2022 Feb 11;11:e68133. doi: 10.7554/eLife.68133. Elife. 2022. PMID: 35147497 Free PMC article.
-
Reliability of cortical activity during natural stimulation.Trends Cogn Sci. 2010 Jan;14(1):40-8. doi: 10.1016/j.tics.2009.10.011. Epub 2009 Dec 11. Trends Cogn Sci. 2010. PMID: 20004608 Free PMC article.
-
Analyzing multicomponent receptive fields from neural responses to natural stimuli.Network. 2011;22(1-4):45-73. doi: 10.3109/0954898X.2011.566303. Epub 2011 Jul 22. Network. 2011. PMID: 21780916 Free PMC article. Review.
References
-
- Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. - PubMed
-
- Albrecht DG, Geisler WS. Motion selectivity and the contrast-response function of simple cells in the visual cortex. Vis Neurosci. 1991;7:531–546. - PubMed
-
- Allman J, Miezin F, McGuinness E. Stimulus specific responses from beyond the classical receptive field: neurophysiological mechanisms for local-global comparisons in visual neurons. Annu Rev Neurosci. 1985;8:407–430. - PubMed
-
- Anzai A, Ohzawa I, Freeman RD. Neural mechanisms for processing binocular information. I. Simple cells. J Neurophysiol. 1999;82:891–908. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
