A flexible sigmoid function of determinate growth

Abstract

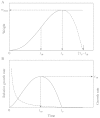
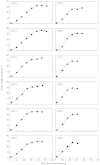
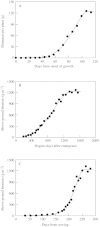
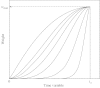
A new empirical equation for the sigmoid pattern of determinate growth, 'the beta growth function', is presented. It calculates weight (w) in dependence of time, using the following three parameters: t(m), the time at which the maximum growth rate is obtained; t(e), the time at the end of growth; and w(max), the maximal value for w, which is achieved at t(e). The beta growth function was compared with four classical (logistic, Richards, Gompertz and Weibull) growth equations, and two expolinear equations. All equations described successfully the sigmoid dynamics of seed filling, plant growth and crop biomass production. However, differences were found in estimating w(max). Features of the beta function are: (1) like the Richards equation it is flexible in describing various asymmetrical sigmoid patterns (its symmetrical form is a cubic polynomial); (2) like the logistic and the Gompertz equations its parameters are numerically stable in statistical estimation; (3) like the Weibull function it predicts zero mass at time zero, but its extension to deal with various initial conditions can be easily obtained; (4) relative to the truncated expolinear equation it provides more reasonable estimates of final quantity and duration of a growth process. In addition, the new function predicts a zero growth rate at both the start and end of a precisely defined growth period. Therefore, it is unique for dealing with determinate growth, and is more suitable than other functions for embedding in process-based crop simulation models to describe the dynamics of organs as sinks to absorb assimilates. Because its parameters correspond to growth traits of interest to crop scientists, the beta growth function is suitable for characterization of environmental and genotypic influences on growth processes. However, it is not suitable for estimating maximum relative growth rate to characterize early growth that is expected to be close to exponential.

Fig. 1. A, Time course of a growth process represented by the beta sigmoid growth function, as shown by the solid line from t = 0 until maximal weight (w_max) is achieved at the end of the growth period (t_e). Hereafter, the weight equals w_max. The dashed line is the mathematical extension of eqn (8) beyond t_e until time (2t_e – t_m), the second intercept of eqn (8) on the time axis. B, The corresponding time course of the absolute growth rate (solid line) and the relative growth rate (dashed line).

Fig. 2. Observed (mean of three sampled culms at each time) time courses (points) and those described by the beta growth function (curve) of grain dry weight for six wheat genotypes (Table 1) grown in glasshouse at two temperatures (Table 2). Estimated parameter values are shown in Table 2. Observed data are from W. Guo (pers. comm.).

Fig. 3. Comparison of maximum grain weight estimated by beta and Gompertz functions (A), and of grain filling duration estimated by beta and truncated expolinear functions (B). Observed experimental data are from W. Guo (pers. comm.). Diagonal broken lines show the 1 : 1 relationship.

Fig. 4. Observed time courses (points) and those described by the beta growth function (curve) of the biomass for the whole maize plant (A, data from Kreusler et al., 1879), for pea crops (B, data from Voisin et al., 2002), and for winter wheat crops (C, data from Gregory et al., 1978). Estimated parameter values are shown in Table 4.

Fig. 5. Illustration of the flexibility of the beta growth function, eqn (8), in representing various sigmoid curves by varying the value of t_m within the range: 0 ≤ t_m < t_e. Curves from the quadratic to a nearly single pulse at t_e correspond to predictions by setting t_m = 0, 0·375t_e, 0·5t_e, 0·625t_e, 0·75t_e, 0·875t_e, 0·95t_e and 0·99975t_e, respectively.