Applying network theory to epidemics: control measures for Mycoplasma pneumoniae outbreaks
- PMID: 12603991
- PMCID: PMC3369603
- DOI: 10.3201/eid0902.020188
Applying network theory to epidemics: control measures for Mycoplasma pneumoniae outbreaks
Abstract
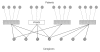
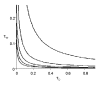
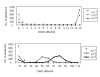
We introduce a novel mathematical approach to investigating the spread and control of communicable infections in closed communities. Mycoplasma pneumoniae is a major cause of bacterial pneumonia in the United States. Outbreaks of illness attributable to mycoplasma commonly occur in closed or semi-closed communities. These outbreaks are difficult to contain because of delays in outbreak detection, the long incubation period of the bacterium, and an incomplete understanding of the effectiveness of infection control strategies. Our model explicitly captures the patterns of interactions among patients and caregivers in an institution with multiple wards. Analysis of this contact network predicts that, despite the relatively low prevalence of mycoplasma pneumonia found among caregivers, the patterns of caregiver activity and the extent to which they are protected against infection may be fundamental to the control and prevention of mycoplasma outbreaks. In particular, the most effective interventions are those that reduce the diversity of interactions between caregivers and patients.
Figures
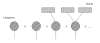



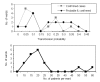

References
-
- Bailey NTJ. The mathematical theory of infectious diseases. New York: Hafner Press; 1975.
-
- May R, Anderson R. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press; 1992.
-
- Hethcote HW. Mathematics of infectious diseases. SIAM Rev. 2000;42:599–653. 10.1137/S0036144500371907 - DOI
-
- Sattenspiel L, Simon CP. The spread and persistence of infectious diseases in structured populations. Math Biosci. 1988;90:341–66. 10.1016/0025-5564(88)90074-0 - DOI
-
- Longini IM. A mathematical model for predicting the geographic spread of new infectious agents. Math Biosci. 1988;90:367–83. 10.1016/0025-5564(88)90075-2 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
