Force generation by actin polymerization II: the elastic ratchet and tethered filaments

Abstract

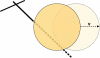
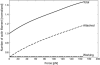
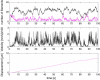
The motion of many intracellular pathogens is driven by the polymerization of actin filaments. The propulsive force developed by the polymerization process is thought to arise from the thermal motions of the polymerizing filament tips. Recent experiments suggest that the nucleation of actin filaments involves a phase when the filaments are attached to the pathogen surface by a protein complex. Here we extend the "elastic ratchet model" of Mogilner and Oster to incorporate these new findings. We apply this "tethered ratchet" model to derive the force-velocity relation for Listeria and discuss relations of our theoretical predictions to experimental measurements. We also discuss "symmetry breaking" dynamics observed in ActA-coated bead experiments, and the implications of the model for lamellipodial protrusion in migrating cells.

FIGURE 1

Sketch of the model. Attached filaments (straight) are nucleated at rate n. They dissociate with rate δ and become “working” filaments (bent). These, in turn, are capped at rate κ. Force balance: the polymerization ratchet force, f_w, generated by the working filaments is balanced by the force of attachment, f_a, and load force, F_L = F_ext + ζV.

FIGURE 2

The right-hand side of Eq. 12 (curve) is plotted as the function of the dimensionless velocity, v. The left-hand side corresponds to the straight line. The intersection gives the steady-state value of v. The nonmonotonic shape of the right-hand side accounts for the biphasic behavior of the load-velocity curve in Fig. 4.

FIGURE 3

The effect of bead size on velocity. Initially, the actin-working filament (solid line) is in contact with the bead surface. As the bead moves forward and the filament grows, the filament (dashed line) eventually grows past the surface and no longer contributes to the propulsion force.

FIGURE 4

The load-velocity curve for Listeria. The solid and dashed curves are computed from the deterministic model. The solid curve corresponds to the parameter values in Table 2. The dashed curve corresponds to a threefold increase in nucleation rate over the solid curve, and illustrates the effect of filament density on the load-velocity behavior. The squares represent the data from the stochastic model simulations corresponding to the parameter values in Table 2, other than V_max = 240 nm/s.

FIGURE 5

Mean field model simulations relating load force to filament density. The number of filaments is normalized to unity at zero load. The solid curve is the number of filaments predicted by the continuous model at varying loads. The dashed curves illustrate that the number of working filaments (horizontal line) is independent of the load, whereas the average number of attached filaments increases with the load.

FIGURE 6

Simulations of the stochastic model. In all three graphs the x axis is time in seconds. (Top) Upper and lower curves show the numbers of working and attached filaments, respectively. (Middle) Velocity in nanometers per second (×100). (Bottom) Cumulative distance traveled in microns.

FIGURE 7

Results of the stochastic model simulations where the filaments grow at the left and right of a bead. In all three graphs, the x axis is time in seconds. (Top panel) Number of cross-links on the right. (Middle panel) Number of cross-links on the left. (Bottom panel) Cumulative distance traveled in nanometers. The bead undergoes an unbiased random walk for almost 500 s, whereupon the number of cross-links at the right fluctuates to zero, whereas the filaments at the left overcome the resistance of the attached filaments, and the bead breaks through the cloud of actin and commences unidirectional motion to the left.

FIGURE 8

Results of the stochastic model simulations with the model parameters described in the text giving the histogram of step-size frequency. The most frequent step size is ∼3–4 nm.