Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2003 Feb 19:2:4.
doi: 10.1186/1475-925x-2-4.

A model of dengue fever

M Derouich  1 , A Boutayeb, E H Twizell
Affiliations

A model of dengue fever

M Derouich et al. Biomed Eng Online. .

Abstract

Background: Dengue is a disease which is now endemic in more than 100 countries of Africa, America, Asia and the Western Pacific. It is transmitted to the man by mosquitoes (Aedes) and exists in two forms: Dengue Fever and Dengue Haemorrhagic Fever. The disease can be contracted by one of the four different viruses. Moreover, immunity is acquired only to the serotype contracted and a contact with a second serotype becomes more dangerous.

Methods: The present paper deals with a succession of two epidemics caused by two different viruses. The dynamics of the disease is studied by a compartmental model involving ordinary differential equations for the human and the mosquito populations.

Results: Stability of the equilibrium points is given and a simulation is carried out with different values of the parameters. The epidemic dynamics is discussed and illustration is given by figures for different values of the parameters.

Conclusion: The proposed model allows for better understanding of the disease dynamics. Environment and vaccination strategies are discussed especially in the case of the succession of two epidemics with two different viruses.

PubMed Disclaimer

Figures

Figure 1
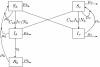
Figure 1
schematic diagram: compartments of human and vector populations
Figure 2
Figure 2
the role of reduction of susceptible humans (Sh) and mosquito population (Nv) to control the disease in the first and second epidemic (model without vaccination (ie p = 0)) Sh = 10000, Nv = 50000 Sh = 2000, Nv = 5000 Sh = 5000, Nv = 50000
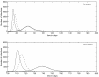
Figure 3
Figure 3
the reduction of the mosquito population is not sufficient to eradicate dengue fever (model without vaccination (ie p = 0)) Nv = 50000 Nv = 30000 Nv = 800
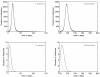
Figure 4
Figure 4
The role of vaccination in the eradication of the disease in the first and second epidemic without vaccination (ie p = 0) p = 0.25 p = 0.75
See this image and copyright information in PMC

References

    1. Derouich M. Modélisation et Simulation de modèles avec et sans structure d'âge : Application au diabète et à la fièvre dengue. PhD thesis Faculty of Sciences, Oujda Morocco. 2001.
    1. Sesser S. Plague proportion. The Asian Wall Street Journal 2002. August 30 Septembre 1.
    1. Dengue and Dengue Haemorrhagic Fever http://www.who.int/inf.fs/en/fact117.html - PubMed
    1. Hethcote HW. The Mathematics of Infectious Diseases. SIAM review. 2000;42:599–653.
    1. Newton EA, Reiter P. A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) Insecticide applications on dengue epidemics. Am J Trop Med Hyg. 1992;47:709–720. - PubMed

Publication types