Buffed energy landscapes: another solution to the kinetic paradoxes of protein folding

Abstract

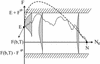
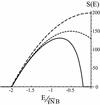
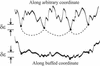
The energy landscapes of proteins have evolved to be different from most random heteropolymers. Many studies have concluded that evolutionary selection for rapid and reliable folding to a given structure that is stable at biological temperatures leads to energy landscapes having a single dominant basin and an overall funnel topography. We show here that, although such a landscape topography is indeed a sufficient condition for folding, another possibility also exists, giving a previously undescribed class of foldable sequences. These sequences have landscapes that are only weakly funneled in the conventional thermodynamic sense but have unusually low kinetic barriers for reconfigurational motion. Traps have been specifically removed by selection. Here we examine the possibility of folding on these "buffed" landscapes by mapping the determination of statistics of pathways for the heterogeneous nucleation processes involved in escaping from traps to the solution of an imaginary time Schroedinger equation. This equation is solved analytically in adiabatic and "soft-wall" approximations, and numerical results are shown for the general case. The fraction of funneled vs. buffed proteins in sequence space is estimated, suggesting the statistical dominance of the funneling mechanism for achieving foldability.

Fig 1.

Nucleation free-energy profiles in trap escape, as a function of the number of escaped residues N_e. Shown are the mean free-energy profile (dashed line) and a typical profile for sequences constrained to have barriers smaller than E+F^≠−(F(b, T)−F^≠). Also shown schematically is the propagator G(F, N_e) for various values of N_e. The system rapidly relaxes to ground-state wavefunction after 𝒪(1) steps (see Appendix).

Fig 2.

Long-dashed line, log number of states vs. energy; solid line, approximate log number of traps from Eq. 11; short-dashed line, log number of traps for the error function expression of f_T in the text above Eq. 11. The approximation is accurate for energies near the ground state but falls off too rapidly for energies near 0. There are still traps at E=0, because states may have positive energies as well. Estimates are used here for the number of states per residue (Ω = e^N×2), system size (N=100), and number of connected states (ν =1). Pair interactions are taken (p=1), energies are in units of B, and δq =1/N.

Fig 3.

Schematic of the energy landscape for a sequence with buffed ground states, projected onto a configurational coordinate. The barriers between the ground states are reduced to F^≠, but the overall variance of energy between states is not reduced. The lowest kinetic barriers between the states determines the escape rate. Along the coordinate(s) where the landscape is buffed, the kinetic barriers between states are reduced.

Fig 4.

The fraction of foldable sequences, on a log scale, as a function of chain length N. Both funneling and buffing mechanisms are shown here. Dashed line, fraction of funneled sequences with forward folding barrier F^≠=4k_BT, and T_F/T_G = 1.6; solid line, fraction of sequences buffed to F^≠=4k_BT. The adiabatic approximation for the Green's function in Eq. 9 is used (see Appendix). The crossover from buffing to funneling suggests the possibility of a compound mechanism for generating a functional protein sequence. The funneling mechanism removes most of the entropy while guiding the protein to a smaller ensemble of similar structures. Then for this reduced collection of states, dynamics between individual traps is most likely mediated by buffing. This dynamics may be related to functionally important motions in proteins (1). For funneled sequences we assume that no ruggedness selection occurs. We scale the Miyazawa–Jernigan interaction parameters so that in our units T_F/T_G ≈ 1.6, a common value taken from the literature (19). Buffed sequences must be selected to be sufficiently rugged to be stable at biological temperatures and must have low kinetic barriers to be accessible on biological time scales. (Inset) Comparison of the fraction of buffed sequences from the adiabatic approximation and from full numerical solution to Eq. 9. Several values of ruggedness are plotted. Circle, b=1.255; triangle, b=1.4; square, b=2.0.