Thirteen years of building constraint-based in silico models of Escherichia coli
- PMID: 12700248
- PMCID: PMC154396
- DOI: 10.1128/JB.185.9.2692-2699.2003
Thirteen years of building constraint-based in silico models of Escherichia coli
Figures

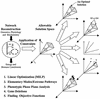
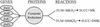
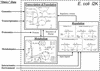
References
-
- Allen, T. E., and B. O. Palsson. 2003. Sequenced-based analysis of metabolic demands for protein synthesis in prokaryotes. J. Theor. Biol. 220:1-18. - PubMed
-
- Blattner, F. R., G. Plunkett 3rd, C. A. Bloch, N. T. Perna, V. Burland, M. Riley, J. Collado-Vides, J. D. Glasner, C. K. Rode, G. F. Mayhew, J. Gregor, N. W. Davis, H. A. Kirkpatrick, M. A. Goeden, D. J. Rose, B. Mau, and Y. Shao. 1997. The complete genome sequence of Escherichia coli K-12. Science 277:1453-1474. - PubMed
-
- Bonarius, H. P. J., G. Schmid, and J. Tramper. 1997. Flux analysis of underdetermined metabolic networks: the quest for the missing constraints. Trends Biotechnol. 15:308-314.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

