Cyclic coordinate descent: A robotics algorithm for protein loop closure
- PMID: 12717019
- PMCID: PMC2323867
- DOI: 10.1110/ps.0242703
Cyclic coordinate descent: A robotics algorithm for protein loop closure
Abstract
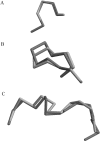
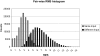
In protein structure prediction, it is often the case that a protein segment must be adjusted to connect two fixed segments. This occurs during loop structure prediction in homology modeling as well as in ab initio structure prediction. Several algorithms for this purpose are based on the inverse Jacobian of the distance constraints with respect to dihedral angle degrees of freedom. These algorithms are sometimes unstable and fail to converge. We present an algorithm developed originally for inverse kinematics applications in robotics. In robotics, an end effector in the form of a robot hand must reach for an object in space by altering adjustable joint angles and arm lengths. In loop prediction, dihedral angles must be adjusted to move the C-terminal residue of a segment to superimpose on a fixed anchor residue in the protein structure. The algorithm, referred to as cyclic coordinate descent or CCD, involves adjusting one dihedral angle at a time to minimize the sum of the squared distances between three backbone atoms of the moving C-terminal anchor and the corresponding atoms in the fixed C-terminal anchor. The result is an equation in one variable for the proposed change in each dihedral. The algorithm proceeds iteratively through all of the adjustable dihedral angles from the N-terminal to the C-terminal end of the loop. CCD is suitable as a component of loop prediction methods that generate large numbers of trial structures. It succeeds in closing loops in a large test set 99.79% of the time, and fails occasionally only for short, highly extended loops. It is very fast, closing loops of length 8 in 0.037 sec on average.
Figures


References
-
- Apaydin, M.S., Guestrin, C.E., Varma, C., Brutlag, D.L., and Latombe, J.C. 2002. Stochastic roadmap simulation for the study of ligand–protein interactions. Bioinformatics 18 Suppl.: S18–S26. - PubMed
-
- Bower, M.J., Cohen, F.E., and Dunbrack Jr., R.L. 1997. Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: A new homology modeling tool. J. Mol. Biol. 267 1268–1282. - PubMed
-
- Briggs, W.L., Henson, V.E., and McCormick, S.F. 2000. A multigrid tutorial. SIAM, Philadelphia.
-
- Bruccoleri, R.E. and Karplus, M. 1987. Prediction of the folding of short polypeptide segments by uniform conformational sampling. Biopolymers 26 137–168. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

