Cooperative regulation of myosin-actin interactions by a continuous flexible chain II: actin-tropomyosin-troponin and regulation by calcium

Abstract

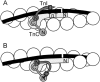
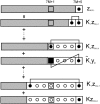
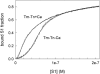
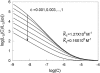
The model of myosin regulation by a continuous tropomyosin chain is generalized to a chain of tropomyosin-troponin units. Myosin binding to regulated actin is cooperative and initially inhibited by the chain as before. In the absence of calcium, myosin is further inhibited by the binding of troponin-I to actin, which through the whole of troponin pins the tropomyosin chain in a blocking position; myosin and TnI compete for actin and induce oppositely-directed chain kinks. The model predicts equilibrium binding curves for myosin-S1 and TnI as a function of their first-order affinities K(S1) and L(TI). Myosin is detached by the actin binding of TnI, but TnI is more efficiently detached by myosin when the kink size (typically nine to ten actin sites) spans the seven-site spacing between adjacent TnI molecules. An allosteric mechanism is used for coupling the detachment of TnI to calcium binding by TnC. With thermally activated TnI kinks (kink energy B approximately k(B)T), TnI also binds cooperatively to actin, producing cooperative detachment of myosin and biphasic myosin-calcium Hill plots, with Hill coefficients of 2 at high calcium and 4-6 at low calcium as observed in striated muscle. The theory also predicts the cooperative effects observed in the calcium loading of TnC.

FIGURE 1

Schematic structure of the regulated actin tropomyosin-troponin (A-Tm-Tn) filament, showing a single chain of tropomyosin (Tm) molecules on one strand of the actin double helix. TnT is bound to one end of Tm and its N-terminus overlaps the adjacent tropomyosin. The C-terminus of TnC and the N-terminal of TnI are bound to TnT. (A) In the absence of calcium, the hands of the N-terminal region of TnC are shut and the C-terminal of TnI is bound to actin and blocks myosin binding to that site. (B) When two calcium ions are bound to TnC, the hands of the N-terminal region are open and bind a region of TnI near its C-terminus, so that the myosin binding site is regulated only by tropomyosin. Based on models of Gagne et al. (1995) and Tripet et al. (1997).

FIGURE 2

The continuous tropomyosin-troponin chain, with troponins bound to the chain at intervals of 38 nm (approximately seven actin sites). All diagrams represent states in the absence of calcium. (A1) In the absence of myosin, most molecules of TnI are bound to actin, locally pinning the chain at a negative angle φ₋ which blocks myosin binding. (A2) The first myosin to bind requires a chain fluctuation allowed by detached TnI molecules or an extreme fluctuation between bound TnI molecules. (A3) At higher myosin density, TnI molecules are detached when the distortion energy of the chain overcomes their binding energy and the chain is forced toward open configurations (φ > φ₊). Under these conditions, additional myosin binding is not locally inhibited by the chain. (B) Cross-sections of the actin filament and tropomyosin chain (•), showing (B1) the TnI binding interface, where bound TnI hangs off the chain at more negative angles (Lehman et al., 2001; Narita et al., 2001) and (B2) the interface for strong myosin binding. The two interfaces overlap so myosin and TnI compete for their binding sites.

FIGURE 3

Diagram illustrating Eq. 7a for components of the myosin-troponin transfer matrix Z_Mk with 7M + k myosin binding sites for k = 5. Every seventh myosin binding site (□) is positioned to bind TnI also. The component , in which the last site is occupied by myosin, can be expressed in terms of for j = 1,…,8 as in I, plus a term where TnI is bound to site 7M + 1 and interacts with the leading myosin through the factor The factor y_M is the component of Z_Mk with site 7M + 1 occupied by TnI and unoccupied sites in front (Eq. 7d; diagram not shown).

FIGURE 4

The fractional occupancies θ, ρ of actin sites by myosin-S1 and troponin-I as functions of their affinities K_S1 and L_TI, predicted for the tropomyosin-troponin chain using A = 1.5 k_BT and ν = 3. The TnI kink energy B is set to zero in A–D and to k_BT in E–F. The bound TnI fraction refers to every seventh actin site, for which myosin and TnI compete.

FIGURE 5

Experimental myosin binding curves versus free S1 concentration for regulated actin systems from skeletal muscle (Maytum et al., 1999), and curves of best-fit to the CFC model for the tropomyosin-troponin chain. The fitted parameters are given in Table 1.

FIGURE 6

Hill plots for myosin bound fraction θ versus free calcium level C. (A) from Fig. 4 A (B = 0), with slopes near unity and (B) from Fig. 4 F (B = 1.5 k_BT), showing biphasic behavior. Abscissas were converted using the equation logL_TI(C) = −12.3−2 log C. The flat region of plots in (A) at low calcium reflect residual myosin binding. To avoid computational singularity, θ_max was set at 1.001.

FIGURE 7

Calcium dependence of the transfer affinity L_TI(C) of TnI from TnC to actin, as predicted from Eq. A1 for λ = 10, ɛ_o = 0, and various values of ɛ. Values of the calcium-binding affinities to TnC are as reported by McKay et al. (2000).

FIGURE 8

Predictions for the mean calcium load of TnC versus calcium concentration C, using the allosteric model of the Appendix, for isolated troponin, and from the chain model for the fully regulated actin filament (A-Tm-Tn) with and without myosin-S1 (K_S1 = 1 and 0). Values of the constants in this model are λ = 10, ɛ_o = 0, and ɛ = 0.001 in all cases; however, the meaning of λ is different in the absence of actin (see main text). Increasing the value of λ favors the open state of TnC and displaces all binding curves to lower calcium. Curves for the actin system were generated by the chain model with βA = 1.5, ν = 3, and βB = 0.01 (A) or 1.0 (B) for TnI kink energy. The corresponding Hill plots (C), (D) show that biphasic behavior is generated in both cases by adding myosin.

Figure 9