Dielectric self-energy in Poisson-Boltzmann and Poisson-Nernst-Planck models of ion channels

Abstract

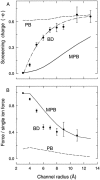
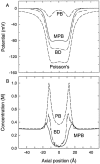
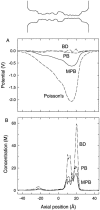
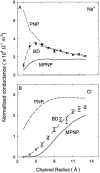
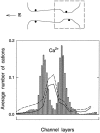
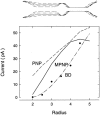
We demonstrated previously that the two continuum theories widely used in modeling biological ion channels give unreliable results when the radius of the conduit is less than two Debye lengths. The reason for this failure is the neglect of surface charges on the protein wall induced by permeating ions. Here we attempt to improve the accuracy of the Poisson-Boltzmann and Poisson-Nernst-Planck theories, when applied to channel-like environments, by including a specific dielectric self-energy term to overcome spurious shielding effects inherent in these theories. By comparing results with Brownian dynamics simulations, we show that the inclusion of an additional term in the equations yields significant qualitative improvements. The modified theories perform well in very wide and very narrow channels, but are less successful at intermediate sizes. The situation is worse in multi-ion channels because of the inability of the continuum theories to handle the ion-to-ion interactions correctly. Thus, further work is required if these continuum theories are to be reliably salvaged for quantitative studies of biological ion channels in all situations.

FIGURE 1

Spurious self-energy contribution to the total potential energy when the ionic charges are distributed continuously. In both cases the charge is contained inside a 4-Å radius sphere and ɛ = 80 is used everywhere. (A) The concentration found using the standard PB equation is plotted against the radial position when there is a net charge of e in the sphere. (B) The energy of the system as the charge in the sphere is increased. Results are shown as found from the PB equation at 298 K (solid line), 0 K (dash-dot line), and as calculated with discrete ions at 0 K (dashed line).

FIGURE 2

Cylindrical channel models used in comparisons of PB and PNP theory with BD simulations. A three-dimensional channel model is generated by rotating the cross section about the central axis by 180°. The cylindrical section is 25 Å in length, and the rounded corners have a radius of curvature of 5 Å, bringing the total length of the channel to 35 Å. The radius of the cylinder r is varied from 3 to 13 Å. The reservoir height h is adjusted so as to keep the total (reservoir and channel) volume constant when the radius is changed.

FIGURE 3

Pore size dependence of the screening charge and force on a cation held at z = 12.5 Å. (A) The net screening charge in the channel (from z = −15 to 15 Å) is plotted as a function of the channel radius. The modified PB (MPB) results are shown by the solid line, standard PB by the dashed line, and the BD values by the solid circles fitted with the dash-dot line. (B) The axial component of the force on the test ion normalized by the force on a single ion (calculated by solving Poisson's equation) is plotted as the channel radius is increased. Symbols are as in A.

FIGURE 4

(A) Potential profiles found in a 4-Å radius cylindrical channel with charges in the protein and no fixed test ion found using the standard PB equation (upper dashed line), modified PB equation (solid line), and BD (dash-dot line) with 300 mM NaCl solution in the baths. The potential found from Poisson's equation with no electrolyte is shown by the lower dashed line. (B) Concentration profiles corresponding to the results in A.

FIGURE 5

(A) Potential and (B) concentration profiles as in Fig. 4 except in the gramicidin A channel. A concentration of 500 mM KCl is used in both cases. The shape of the channel is shown in the inset.

FIGURE 6

(A) Potential and (B) concentration profiles as in Fig. 4 except in the KcsA potassium channel. A concentration of 300 mM KCl is used in both cases. The shape of the channel is indicated in the inset.

FIGURE 7

Conductance of Na⁺ (A) and Cl⁻ (B) ions for bare (no fixed charge) channels of varying radii normalized by the cross-sectional area. The results of the modified PNP equations (solid lines), standard PNP (dashed lines), and BD simulations (data points fitted by dash-dot lines) are shown. The ions are driven across the channel with an applied field of 105 mV between the reservoir ends and a 300 mM NaCl solution is maintained in the reservoirs.

FIGURE 8

Normalized conductance in cylindrical channels with fixed charges in the channel walls; otherwise, as in Fig. 7.

FIGURE 9

Concentration profiles for (A) Na⁺ and (B) Cl⁻ ion in a 4-Å radius cylindrical channel with fixed charges as found from the modified PNP equations (solid line), standard PNP (dashed line), and BD simulations (bars). The pore is divided into 16 equal segments along the channel axis, and the average concentration in each segment is plotted.

FIGURE 10

Current-concentration relationships for (A) CaCl₂ and (B) NaCl in the L-type calcium channel. Results found from BD simulations (data points fitted by dash-dot line), the standard PNP equations (dashed line), and the modified PNP equations (solid line) are shown. The shape of the channel and the locations of two of the four glutamate residues (squares), and the negative ends of the intracellular helix dipoles (diamonds) are shown in the inset. Diffusion coefficients used are 1.33 and 0.79 × 10⁻⁹ m² s⁻¹ for sodium and calcium.

FIGURE 11

Average number of ions in layers comprising the right-half of the calcium channel as found from BD simulations (bars) as well as the standard (dashed line) and modified (solid line) PNP equations using 150 mM CaCl₂. The section of the channel for which the concentration is plotted is indicated by the dashed box in the inset.

FIGURE 12

Current passing through the simplified potassium channel model plotted against the intracellular pore radius of the channel as found from BD simulations (data points fitted by dash-dot line), the standard (dashed line), and modified (solid line) PNP equations. The shape of the channel is shown in the inset.