Azimuthal frustration and bundling in columnar DNA aggregates
- PMID: 12770870
- PMCID: PMC1302946
- DOI: 10.1016/S0006-3495(03)75092-9
Azimuthal frustration and bundling in columnar DNA aggregates
Abstract
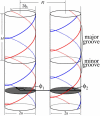
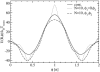
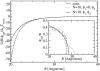
The interaction between two stiff parallel DNA molecules is discussed using linear Debye-Hückel screening theory with and without inclusion of the dielectric discontinuity at the DNA surface, taking into account the helical symmetry of DNA. The pair potential furthermore includes the amount and distribution of counterions adsorbed on the DNA surface. The interaction does not only depend on the interaxial separation of two DNA molecules, but also on their azimuthal orientation. The optimal mutual azimuthal angle is a function of the DNA-DNA interaxial separation, which leads to azimuthal frustrations in an aggregate. On the basis of the pair potential, the positional and orientational order in columnar B-DNA assemblies in solution is investigated. Phase diagrams are calculated using lattice sums supplemented with the entropic contributions of the counterions in solution. A variety of positionally and azimuthally ordered phases and bundling transitions is predicted, which strongly depend on the counterion adsorption patterns.
Figures

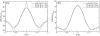












Similar articles
-
Phase behavior of columnar DNA assemblies.Phys Rev Lett. 2002 Jul 1;89(1):018303. doi: 10.1103/PhysRevLett.89.018303. Epub 2002 Jun 17. Phys Rev Lett. 2002. PMID: 12097075
-
Nonlinear effects in the torsional adjustment of interacting DNA.Phys Rev E Stat Nonlin Soft Matter Phys. 2004 Apr;69(4 Pt 1):041905. doi: 10.1103/PhysRevE.69.041905. Epub 2004 Apr 29. Phys Rev E Stat Nonlin Soft Matter Phys. 2004. PMID: 15169041
-
Attraction between DNA molecules mediated by multivalent ions.Phys Rev E Stat Nonlin Soft Matter Phys. 2004 Apr;69(4 Pt 1):041904. doi: 10.1103/PhysRevE.69.041904. Epub 2004 Apr 28. Phys Rev E Stat Nonlin Soft Matter Phys. 2004. PMID: 15169040
-
Static and dynamic heterogeneities in water.Philos Trans A Math Phys Eng Sci. 2005 Feb 15;363(1827):509-23. doi: 10.1098/rsta.2004.1505. Philos Trans A Math Phys Eng Sci. 2005. PMID: 15664896 Review.
-
The contribution of transient counterion imbalances to DNA bending fluctuations.Biophys J. 2006 May 1;90(9):3208-15. doi: 10.1529/biophysj.105.078865. Epub 2006 Feb 3. Biophys J. 2006. PMID: 16461401 Free PMC article. Review.
Cited by
-
Local structure of DNA toroids reveals curvature-dependent intermolecular forces.Nucleic Acids Res. 2021 Apr 19;49(7):3709-3718. doi: 10.1093/nar/gkab197. Nucleic Acids Res. 2021. PMID: 33784405 Free PMC article.
-
Structural investigations of DNA-polycation complexes.Eur Phys J E Soft Matter. 2005 Jan;16(1):17-28. doi: 10.1140/epje/e2005-00003-4. Epub 2005 Jan 31. Eur Phys J E Soft Matter. 2005. PMID: 15688137
-
Formation of impeller-like helical DNA-silica complexes by polyamines induced chiral packing.Interface Focus. 2012 Oct 6;2(5):608-16. doi: 10.1098/rsfs.2011.0119. Epub 2012 Feb 22. Interface Focus. 2012. PMID: 24098845 Free PMC article.
-
Order and interactions in DNA arrays: Multiscale molecular dynamics simulation.Sci Rep. 2017 Jul 6;7(1):4775. doi: 10.1038/s41598-017-05109-2. Sci Rep. 2017. PMID: 28684875 Free PMC article.
References
-
- Allahyarov, E., and H. Löwen. 2000. Effective interaction between helical biomolecules. Phys. Rev. E. 62:5542–5556. - PubMed
-
- Ashcroft, N. W., and D. Stroud. 1978. Theory of the thermodynamics of simple liquid metals. Sol. State Phys. 33:1–81.
-
- Bloomfield, V. A. 1996. DNA condensation. Curr. Opin. Struct. Biol. 6:334–341. - PubMed
-
- Canessa, E., M. J. Grimson, and M. Silbert. 1988. Volume dependent forces in charge stabilized colloidal crystals. J. Mol. Phys. 64:1195–1201.
-
- Denton, A. R. 1999. Effective interactions and volume energies in charge-stabilized colloidal suspensions. J. Phys.: Condens. Matter 11:10061–10071; 2000.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

