The role of the dielectric barrier in narrow biological channels: a novel composite approach to modeling single-channel currents

Abstract

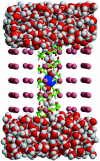
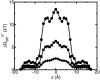
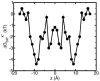
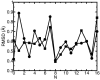
A composite continuum theory for calculating ion current through a protein channel of known structure is proposed, which incorporates information about the channel dynamics. The approach is utilized to predict current through the Gramicidin A ion channel, a narrow pore in which the applicability of conventional continuum theories is questionable. The proposed approach utilizes a modified version of Poisson-Nernst-Planck (PNP) theory, termed Potential-of-Mean-Force-Poisson-Nernst-Planck theory (PMFPNP), to compute ion currents. As in standard PNP, ion permeation is modeled as a continuum drift-diffusion process in a self-consistent electrostatic potential. In PMFPNP, however, information about the dynamic relaxation of the protein and the surrounding medium is incorporated into the model of ion permeation by including the free energy of inserting a single ion into the channel, i.e., the potential of mean force along the permeation pathway. In this way the dynamic flexibility of the channel environment is approximately accounted for. The PMF profile of the ion along the Gramicidin A channel is obtained by combining an equilibrium molecular dynamics (MD) simulation that samples dynamic protein configurations when an ion resides at a particular location in the channel with a continuum electrostatics calculation of the free energy. The diffusion coefficient of a potassium ion within the channel is also calculated using the MD trajectory. Therefore, except for a reasonable choice of dielectric constants, no direct fitting parameters enter into this model. The results of our study reveal that the channel response to the permeating ion produces significant electrostatic stabilization of the ion inside the channel. The dielectric self-energy of the ion remains essentially unchanged in the course of the MD simulation, indicating that no substantial changes in the protein geometry occur as the ion passes through it. Also, the model accounts for the experimentally observed saturation of ion current with increase of the electrolyte concentration, in contrast to the predictions of standard PNP theory.

FIGURE 1

Snapshot of the GA channel with a K⁺ ion embedded in a model membrane and solvated with water after a 300-ps MD simulation as described in text. The model lipid bilayer is represented by pink spheres (the radius of the pink sphere in a picture does not reflect its Lennard-Jones parameters). The K⁺ ion is shown as the blue sphere in the center of the channel. Only backbone atoms of the peptide chains are shown.

FIGURE 2

Two-dimensional center cut of the three-dimensional space-dependent dielectric constant function used for numerical solution of the Poisson equation. The simulation system is divided into four regions: the protein (ɛ_p), the bulk water (ɛ_w), the membrane (ɛ_m), and the channel water ().

FIGURE 3

Electrostatic free energy of the K⁺-GA binding, , is calculated here for a rigid channel with different protein dielectric constants). is plotted as a function of the ion displacement from the center of the GA channel along the channel axis. The energy is calculated by numerical solution of the Poisson equation for a configuration of GA taken from the PDB data bank (Arsen'ev et al., 1986) (Eqs. 5–6). The dielectric constant of the bulk water is ɛ_w = 80, the membrane ɛ_m = 4 and the channel water = 80. The dielectric constant of the protein was taken to be ɛ_p = 4 (•), 10 (▪), and 30 (♦). See Fig. 2 for the assignment of regions with different dielectric constants.

FIGURE 4

calculated for different protein structures which are collected during the MD simulation. Note how the energy fluctuates between positive and negative values, indicating ion-permeable and impermeable structural conformations of the protein (see explanation in text). In both panels = 40, ɛ_w = 80, and ɛ_m = 4. (a) Initial relaxation. ɛ_p = 2. (b) A portion of the equilibrium trajectory. Solid line shows calculations with ɛ_p = 4, and dashed line is for ɛ_p = 2.

FIGURE 5

(a) Dependence of on plotted for several snapshots taken from the MD trajectory; n is the index labeling snapshots along the MD trajectory. The following set of dielectric parameters was used ɛ_p = ɛ_m = 4, ɛ_w = = 80. The dielectric constant of the channel water was set to = 20 (♦), 40 (▪), and 80 (•). See Fig. 2 for the assignment of regions with different dielectric constants. (b) Dependence of on ɛ_m plotted for several snapshots taken from the MD trajectory. The following set of dielectric parameters was used ɛ_p = 2, ɛ_w = 80, = 40. The dielectric constant of the membrane was set to ɛ_m = 2 (♦) and 4 (•).

FIGURE 6

The total free energy profile calculated for K⁺ ion in the channel using the flexible channel with fluctuations generated by an MD trajectory as described in “A Combined Molecular Dynamics/Continuum Electrostatics Approach to Calculate Free Energy”. Each point in the plot is the average of N = 150 calculations along the 300-ps MD trajectory as prescribed by Eq 7. The following set of dielectric parameters was used: ɛ_p = ɛ_m = 4, ɛ_w = = 80.

FIGURE 7

(a) Average free energy of K⁺, flexible GA binding i.e., with partial charges on GA atoms (•), compared with i.e., without partial charges on the GA atoms (♦). Each point is the average of N = 150 calculations along the 300-ps MD trajectory as prescribed by Eq. 7. (b) The same as in a but for the rigid NMR geometry of GA as prescribed by Eq. 5. (c) The same as in b but for average MD geometry of GA equilibrated with only water (no ion) in the channel.

FIGURE 8

Root mean square deviation of GA backbone carbonyl oxygen atoms in the MD simulation. The numbers of the residues in the protein sequence are indicated on the abscissa. Circles correspond to the simulation with a K⁺ ion placed in the center of the channel (•). The curve with the squares is for the GA channel without K⁺ (▪). Each root mean square deviation curve is calculated along the 300-ps MD trajectory relative to the corresponding average MD structure.

FIGURE 9

The average configuration of GA in MD simulation without the ion (orange peptide) is superimposed with the average configuration of GA in MD simulations with the K⁺ ion (green peptide). K⁺ is shown as a blue sphere. Arrows indicate the carbonyl oxygens that bend toward the K⁺ due to favorable electrostatic interactions. (a) During the MD simulation, an ion was in the center of the channel; and (b) K⁺ is 9 Å from the center of the channel, the predicted position of the binding site (cf. Fig. 6).

FIGURE 10

Average for a flexible GA (•) and for a rigid one (♦). For the flexible protein each point in the plot is the average of N = 150 calculations along the 300-ps MD trajectory as prescribed by Eq. 7. The NMR geometry of the GA was used for the rigid channel. The following set of dielectric parameters was used for both calculations: ɛ_p = ɛ_m = 4, ɛ_w = = 80.

FIGURE 11

Calculated diffusion coefficient for K⁺ ion inside of the GA channel (•), and in bulk SPC/E water (solid line). Only the D_z component of the diffusion coefficient of the ion in the channel is calculated.

FIGURE 12

Current-voltage relations predicted by PMFPNP model are compared to experimental results (Busath et al., 1998) (upper left inset). Bulk KCl concentrations of 0.1 (shaded square) and 1.0 M (open circle) were used in the simulations. The experimental curves in the inset correspond to the following concentrations of bulk KCl solutions: shaded square, 0.1 M; solid circle, 0.2 M; open square, 0.5 M; open circle, 1.0 M; and solid square, 2.0 M. The analogous experimental and calculated curves are labeled with the same symbols.

FIGURE 13

Current-concentration relations as predicted by PNP (♦) and PMFPNP (•) models. The external potential difference was set to 100 mV.

FIGURE 14

profile along the channel axes for K⁺ and Cl⁻ is plotted for several bulk electrolyte concentrations and 100 mV applied voltage: a and c were calculated using PNP; b and d were calculated using PMFPNP. The curve with circles is for 0 M, the curve with squares is for 0.5 M, and the curve with diamonds is for 10 M electrolyte concentrations. The dashed line is the result of a calculation at OM electrolyte concentration in which the protein molecule has no partial charges on the atoms. It corresponds to the linear ramp potential caused by the high resistivity of the membrane.

FIGURE 15

Ion concentration profile along the channel axis for K⁺ and Cl⁻ is plotted for several bulk electrolyte concentrations: a and c were calculated using PNP; b and d were calculated using PMFPNP. The curves with diamonds and circles are for 0.5 M; the curves with squares and triangles are for 10 M electrolyte concentrations.