The effect of lipid demixing on the electrostatic interaction of planar membranes across a salt solution

Abstract

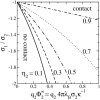
We study the effect of lipid demixing on the electrostatic interaction of two oppositely-charged membranes in solution, modeled here as an incompressible two-dimensional fluid mixture of neutral and charged mobile lipids. We calculate, within linear and nonlinear Poisson-Boltzmann theory, the membrane separation at which the net electrostatic force between the membranes vanishes, for a variety of different system parameters. According to Parsegian and Gingell, contact between oppositely-charged surfaces in an electrolyte is possible only if the two surfaces have exactly the same charge density (sigma(1) = -sigma(2)). If this condition is not fulfilled, the surfaces can repel each other, even though they are oppositely charged. In our model of a membrane, the lipidic charge distribution on the membrane surface is not homogeneous and frozen, but the lipids are allowed to freely move within the plane of the membrane. We show that lipid demixing allows contact between membranes even if there is a certain charge mismatch, /sigma(1)/ not equal /sigma(2)/, and that in certain limiting cases, contact is always possible, regardless of the value of sigma(1)/sigma(2) (if sigma(1)/sigma(2) < 0). We furthermore find that of the two interacting membranes, only one membrane shows a major rearrangement of lipids, whereas the other remains in exactly the same state it has in isolation and that, at zero-disjoining pressure, the electrostatic mean-field potential between the membranes follows a Gouy-Chapman potential from the more strongly charged membrane up to the point of the other, more weakly charged membrane.

FIGURE 1

Schematic view of our model of two membranes. The membranes interact only locally via interaction zones, assumed to be planar and parallel surfaces, located at x = 0 (membrane 1) and x = l (membrane 2). We consider only electrostatic interactions. Outside the interaction zones, the membranes are characterized by their surface potentials (), their surface-charge densities (σ_i), the valency of the lipidic charges (q_i), and the surface fraction of charged lipids (η_i) (i = 1,2). In our model, we allow lipids to freely flow between the interaction zones and those parts of the membrane not involved in the interaction (reservoir), so the surface potentials in the interaction zone (Φ(0) for membrane 1 and Φ(l) for membrane 2) as well as the surface charge densities ( and ) can be different from their corresponding values in the reservoir.

FIGURE 2

Regions of attraction and repulsion between two oppositely-charged membranes consisting of immobile lipids (a) and mobile lipids (b and c), as a function of the intermembrane distance and the ratio of surface charge densities. Fig. 2, b and c show the line of zero net force for four different values of the surface fraction of charged lipids η₂ (η₂ = 1, 0.75, 0.5, and 0.25, from top to bottom for the curves in the un-hatched region). The sign of the effective intermembrane force in the hatched region of the parameter space can be inferred from a corresponding point in the un-hatched region.

FIGURE 3

Regions in parameter space where touching contact (κl = 0) between two oppositely-charged membranes corresponds to the equilibrium configuration, as a function of σ₁/σ₂ and the surface fraction η₂ of mobile lipids on the membrane with the lower surface densities of lipids. The dashed line is the function −1/η₂. See text for details.

FIGURE 4

Regions in parameter space where touching contact between oppositely-charged membranes is energetically allowed. Plot is similar to that in Fig. 3, but now the parameter space is spanned by σ₁/σ₂ and , while η₂ is fixed to 0.1, 0.3, 0.5, 0.7, and 0.9. Variation of can be experimentally realized by controlling the salt concentration in the electrolyte solution. State points to the left of the curves correspond to systems where touching contact between the membranes is energetically impossible; those to the right, energetically possible. Reducing the salt concentration in the electrolyte can cause membranes to make contact.

FIGURE 5

Regions of attraction and repulsion between oppositely-charged lipid membranes, for various combinations of η₂ and . Plots are similar to Fig. 2, but now with the zero-pressure line determined from the nonlinear Poisson-Boltzmann equation. The order of the values of the varied quantity corresponds to the order of the curves from top to bottom. The thin solid line is the function giving the zero-pressure state line for η₂ = 1.0 in linear theory (see Eq. 18).

FIGURE 6

Same as in Fig. 3, but now the zero-pressure state lines are calculated within the nonlinear Poisson-Boltzmann theory. For comparison, the state line depicted in Fig. 3 is given as a thin solid line. The other curves (from top to bottom) correspond to values of = 0.2, 0.4, 0.5, 1.0, and 2.0. Pairs of membranes with state points lying to the right of the curves will repel each other at contact. The dashed line is the function −1/η₂ which the zero-pressure lines approach in the limit .