FRET or no FRET: a quantitative comparison
- PMID: 12770904
- PMCID: PMC1302980
- DOI: 10.1016/S0006-3495(03)75126-1
FRET or no FRET: a quantitative comparison
Abstract
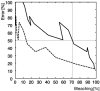
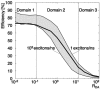
Fluorescence resonance energy transfer (FRET) is a technique used to measure the interaction between two molecules labeled with two different fluorophores (the donor and the acceptor) by the transfer of energy from the excited donor to the acceptor. In biological applications, this technique has become popular to qualitatively map protein-protein interactions, and in biophysical projects it is used as a quantitative measure for distances between a single donor and acceptor molecule. Numerous approaches can be found in the literature to quantify and map FRET, but the measures they provide are often difficult to interpret. We propose here a quantitative comparison of these methods by using a surface FRET system with controlled amounts of donor and acceptor fluorophores and controlled distances between them. We support the system with a Monte Carlo simulation of FRET, which provides reference values for the FRET efficiency under various experimental conditions. We validate a representative set of FRET efficiencies and indices calculated from the different methods with different experimental settings. Finally, we test their sensitivity and draw conclusions for the preparation of FRET experiments in more complex and less-controlled systems.
Figures
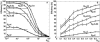
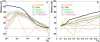

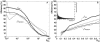



References
-
- Arai, R., H. Ueda, K. Tsumoto, W. C. Mahoney, I. Kumagai, and T. Nagamune. 2000. Fluorolabeling of antibody variable domains with green fluorescent protein variants: application to an energy transfer-based homogeneous immunoassay. Protein. Eng. 13:369–376. - PubMed
-
- Bottiroli, G., A. C. Croce, and R. Ramponi. 1992. Fluorescence resonance energy transfer imaging as a tool for in situ evaluation of cell morphofunctional characteristics. J. Photochem. Photobiol. B. 12:413–416. - PubMed
-
- Chan, F. K., R. M. Siegel, D. Zacharias, R. Swofford, K. L. Holmes, R. Y. Tsien, and M. J. Lenardo. 2001. Fluorescence resonance energy transfer analysis of cell surface receptor interactions and signaling using spectral variants of the green fluorescent protein. Cytometry. 44:361–368. - PubMed
-
- Clegg, R. 1996. Fluorescence resonance energy transfer. In Fluorescence Imaging Spectroscopy and Microscopy. X. F. Wang and B. Herman, editors. John Wiley, New York. 179–252.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

