Properties of single voltage-gated proton channels in human eosinophils estimated by noise analysis and by direct measurement

Abstract

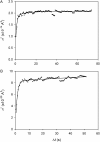
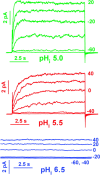
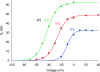
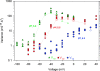
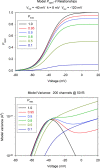
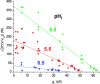
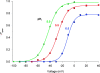
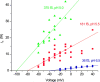
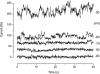
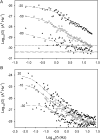
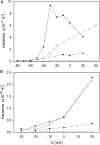
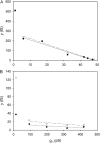
Voltage-gated proton channels were studied under voltage clamp in excised, inside-out patches of human eosinophils, at various pHi with pHo 7.5 or 6.5 pipette solutions. H+ current fluctuations were observed consistently when the membrane was depolarized to voltages that activated H+ current. At pHi < or = 5.5 the variance increased nonmonotonically with depolarization to a maximum near the midpoint of the H+ conductance-voltage relationship, gH-V, and then decreased, supporting the idea that the noise is generated by H+ channel gating. Power spectral analysis indicated Lorentzian and 1/f components, both related to H+ currents. Unitary H+ current amplitude was estimated from stationary or quasi-stationary variance, sigmaH2. We analyze sigmaH2 data obtained at various voltages on a linearized plot that provides estimates of both unitary conductance and the number of channels in the patch, without requiring knowledge of open probability. The unitary conductance averaged 38 fS at pHi 6.5, and increased nearly fourfold to 140 fS at pHi 5.5, but was independent of pHo. In contrast, the macroscopic gH was only 1.8-fold larger at pHi 5.5 than at pHi 6.5. The maximum H+ channel open probability during large depolarizations was 0.75 at pHi 6.5 and 0.95 at pHi 5.5. Because the unitary conductance increases at lower pHi more than the macroscopic gH, the number of functional channels must decrease. Single H+ channel currents were too small to record directly at physiological pH, but at pHi < or = 5.5 near Vthreshold (the voltage at which gH turns on), single channel-like current events were observed with amplitudes 7-16 fA.

Figure 1.

Effect of sample length (Δt) on estimates of the current variance (σ ²). (A) pH_o//pH_i 7.5//5.0, V = −30 mV; the curve is a least-squares fit of with A ₀ = 4.0 × 10⁻²⁷ A², A ₁ = 1.5 × 10⁻²⁶ A², A ₂ = 2.0 × 10⁻²⁷ A², τ ₁ = 1.1 s and τ ₂ = 9.3 s. (B) pH_o//pH_i 7.5//6.5, V = 10 mV; the curve is a least-squares fit of , with A ₀ = 7.2 × 10⁻²⁹ A², A ₁ = 7.6 × 10⁻²⁸ A², τ ₁ = 1.3 s and B = 1.3 × 10⁻³⁰ A² s⁻¹. See text for details.

Figure 2.

Current fluctuations occur at voltages that activate voltage-gated proton current. Families of currents at pH_o 7.5 and three pH_i in the same membrane patch are illustrated at the same time and current calibrations. Raw currents are shown at 20-mV intervals, as indicated, with no leak correction. The holding potential was −100 mV at pH_i 5.0 and −80 mV for pH_i 5.5. The currents shown were obtained at 11–46 min for pH_i 6.5, 81 min for pH_i 5.5, and 83 min for pH_i 5.0, respectively, after patch excision. Filter was 20 Hz for all. ES-2596.

Figure 3.

Steady-state g _H-V relationships for the patch illustrated in Fig. 2. Chord conductance, g _H, was calculated assuming V _rev of −40, −80, and −100 mV, at pH_i 6.5 (•), 5.5 (▪), and 5.0 (▴), respectively. Curves show best-fitting (by nonlinear least squares) Boltzmann functions: g _H = g _H,max {1 + exp[−(V − V _1/2)/k]}⁻¹ with midpoints (V _1/2) of −10.4, −26.9, and −43.0 mV, slope factors (k) of 5.2, 7.8, and 8.1 mV, and g _H,max of 32.6, 48.7, and 62.2 pS at pH_i 6.5, 5.5, and 5.0, respectively. ES-2596.

Figure 4.

Voltage dependence of total variance from the same patch as Figs. 2 and 3. Symbols have the same meaning. The midpoints of the P _open-voltage relationships determined as described in Fig. 7, are indicated by symbols near the X axis. The open symbols show the band-limited Lorentzian component of the σ² in this experiment, , obtained by fitting power spectra with Lorentzian plus 1/f components (as described in Fig. 10). There is divergence only at large depolarizations at pH_i 5.0, where the 1/f component became significant. ES-2596.

Figure 5.

Model showing the voltage dependence of variance in a simple two-state channel, for different values of P _max, the maximum P _open during large depolarizations. The top panel shows the assumed P _open-V relationships with various P _max values, as indicated. All were calculated from a Boltzmann function with midpoint, V _1/2 = −40 mV and slope factor, k = 8 mV. The bottom panel shows the variance expected for 200 channels with γ_H 50 fS and V _rev −120 mV, assuming the various P _open-V relationships plotted above. The curves were generated using Eq. 1 with I _H = i _H N P _open = γ_H (V − V _rev) N P _open.

Figure 6.

Simultaneous estimation of γ_H and N at three pH_i in the same patch and with the same symbol meanings as in Figs. 2–4. The data set includes many records and different voltages. The lines are least-squares fits of Eq. 2, in which the Y-intercept is γ_H and the slope is −1/N, providing the following estimates: γ_H 36 fS, 181 fS, and 375 fS, and N 1210, 290, and 170 for pH_i 6.5, 5.5, and 5.0, respectively. ES-2596.

Figure 7.

Voltage dependence of P _open at pH_i 6.5, 5.5, and 5.0, for the same patch as in Figs. 2–4, and 6. P _open was estimated as g _H/(N γ _H), where the total number of channels in the patch, N, and γ_H were estimated from the y-g_H plot (Fig. 6). Here only the last 1–2 records at each voltage are included, because earlier points were farther from steady-state. Curves show best-fitting (by nonlinear least squares) Boltzmann functions: P _open = P _max {1 + exp[−(V − V _1/2)/k]}⁻¹ with midpoints (V _1/2) of −11.2, −26.9, and −42.9 mV, slope factors (k) of 5.7, 7.8, and 8.3 mV, and P _max of 0.78, 0.93, and 0.98 at pH_i 6.5, 5.5, and 5.0, respectively. ES-2596.

Figure 8.

Single H⁺ channel current-voltage plots in the same patch and with the same symbol meanings as in Figs. 2–4 and 6 and 7. Estimates for i _H were obtained by using Eq. 1, where P _open is derived from the analysis in Fig. 7, and ultimately from the estimates of γ_H and N obtained from the y-g_H plot (Fig. 6). ES-2596.

Figure 9.

Apparent single proton channel currents at pH_o 7.5 and pH_i 5.5. These currents were filtered at 20 Hz (8-pole Bessel) and later digitally refiltered at 10 Hz. The current scale is positioned arbitrarily. The resistance of this patch at subthreshold voltages was 5 TΩ. For clarity, each record is displaced vertically by 20 fA above its true position relative to the record underneath. ES2724.

Figure 10.

Power spectra of H⁺ current fluctuations. Test voltages (mV) are shown next to each curve. (A) pH_o = 7.5, pH_i = 5.5, V _threshold = −55 mV. The subthreshold data (▴) are fitted with a 1/f spectrum while the suprathreshold data sets are fitted with Lorentzian plus 1/f spectra. The latter two data sets can be fitted equally well by a Lorentzian plus white noise. The horizontal lines show the calculated sum of the spectral densities of the calculated shot noise of current flow and Johnson noise of the 50 GΩ feedback resistor in parallel with the patch resistance, which were: 3.8 × 10⁻³¹ (▴), 4.4 × 10⁻³¹ (○) and 1.7 × 10⁻³⁰ (▾) A² Hz⁻¹. (B) pH_o = 7.5, pH_i = 6.5, V _threshold < −30 mV. The near-threshold data (▴) are fitted with a Lorentzian plus white noise while the other datasets are each fitted with a Lorentzian plus 1/f plus white noise. The data at −10 and 20 mV can be fitted equally well with a 1/f spectrum plus white noise, but the exponents (m) on f are significantly greater than unity (1.29 ± 0.05 and 1.37 ± 0.07, respectively). The sum of Johnson- and shot-noise spectral densities were 1.3 × 10⁻³⁰ (▴), 8.4 × 10⁻³⁰ (○) and 2.0 × 10⁻²⁹ (▾) A² Hz⁻¹ (too small to show on this scale). Data in A and B are from two different patches (ES-2596, ES-2579).

Figure 11.

The Lorentzian variance (▴) and the band-limited 1/f (○) and white noise (▾) variances were determined from fitted power spectra (Fig. 10) and are plotted here against membrane voltage (V). The white noise and 1/f variances were calculated over the interval [f ₀, f _N], where f ₀ is the lowest frequency in the spectrum and f _N is the Nyquist frequency. On average, the band-limited Lorentzian variance (open symbols in Fig. 4) was ∼10% less than the total Lorentzian variance (which is plotted here). The dashed lines without symbols show the calculated sum of the Johnson- and shot-noise variances (see Fig. 10) over the interval [f ₀, f _N]. (A) pH_o = 7.5, pH_i = 5.5, V _threshold = −55 mV; (B) pH_o = 7.5, pH_i = 6.5, V _threshold < −30 mV. Same two patches as in Fig. 10. In A, 1/f noise was not detectable between −10 and 20 mV; presumably it was masked by the Lorentzian. On the other hand, only 1/f noise was detected at 40 mV; apparently Lorentzian noise had fallen to undetectable levels, suggesting a P _max value close to unity. In B, no peak is observed in the Lorentzian variance, suggesting P _max ≤ 0.8 (see text and Fig. 5).

Figure 12.

Examples of y-g _H plots with y calculated using the total variance (○, dashed line) or the Lorentzian variance (•, solid line). See Eqs 2 and 3. (A) pH_o 7.5, pH_i 5.5; (B) pH_o 7.5, pH_i 6.5. Same two patches as in Figs. 10 and 11. Regression lines were fitted after omitting the outliers near g _H = 0. In B, the slopes are not statistically significant, illustrating the difficulty of estimating N (= −1/slope) at pH_i 6.5. However, more reliable estimates of N were obtained in some cases (e.g., Fig. 6).

Figure 13.

Comparison of the Lorentzian time constants (τ _L), single-channel mean open times, and time constants of H⁺ current activation (τ _act) and deactivation (τ _tail) at various pH_o and pH_i. Mean open time is the global mean of data at −60 mV from five patches (n = 9–33 in each patch), estimated from current records like those in Fig. 9, in which apparently discrete single-channel events occurred near V _threshold, all filtered at 10–20 Hz. τ _act was determined by fitting the function I = I _max [1 − exp(−t/τ _act)] to I(t) curves such as those in Fig. 2 (top two panels). Mean values of τ _act for P _open = 0.5P _max are compared with mean values of τ _L (which showed no consistent dependence on P _open). Bars show standard errors from 2–4 patches; no error bars indicate only one patch was available. τ _tail at V < V _rev was determined by fitting a single exponential to tail currents recorded ∼10 mV negative to V _rev (mean ± SE, n = 8–18 for each pH). Also shown are τ _tail values extrapolated to the midpoint voltage of the g _H-V relationship, assuming exponential voltage dependence with a slope of 40 mV/e-fold change in τ _tail.