Self-organizing neural integrator predicts interval times through climbing activity

Abstract

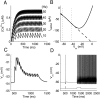
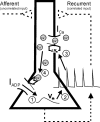
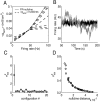
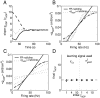
Mammals can reliably predict the time of occurrence of an expected event after a predictive stimulus. Climbing activity is a prominent profile of neural activity observed in prefrontal cortex and other brain areas that is related to the anticipation of forthcoming events. Climbing activity might span intervals from hundreds of milliseconds to tens of seconds and has a number of properties that make it a plausible candidate for representing interval time. A biophysical model is presented that produces climbing, temporal integrator-like activity with variable slopes as observed empirically, through a single-cell positive feedback loop between firing rate, spike-driven Ca2+ influx, and Ca2+-activated inward currents. It is shown that the fine adjustment of this feedback loop might emerge in a self-organizing manner if the cell can use the variance in intracellular Ca2+ fluctuations as a learning signal. This self-organizing process is based on the present observation that the variance of the intracellular Ca2+ concentration and the variance of the neural firing rate and of activity-dependent conductances reach a maximum as the biophysical parameters of a cell approach a configuration required for temporal integration. Thus, specific mechanisms are proposed for (1) how neurons might represent interval times of variable length and (2) how neurons could acquire the biophysical properties that enable them to work as timers.

Figure 1.

Basic model properties. A, Accumulation of internal Ca²⁺ in the model cell at different (output) spiking rates. The average level of [Ca²⁺]_i increases linearly with spike rate, as found by Helmchen et al. (1996). B, I_NMDA as a function of voltage (solid line). Between E_leak (-65 mV) and firing threshold (less than -45 mV), I_NMDA is well described by a linear fit (dashed line). C, Train of EPSPs elicited by presynaptic stimulation at 20 Hz. EPSP amplitude decreases over time as described by the model of Tsodyks and Markram (1997) and Markram et al. (1998). D, Response of the model cell to brief (5 msec) or longer-lasting (250 msec) current injections. A brief current pulse elicits a single spike followed by an after depolarizing potential caused by g_ADP. Longer current pulses drive the cell in to a persistent spiking up state maintained by Ca²⁺-activated g_ADP. (Note that spike generation is not explicitly modeled in an LIF-model, and spikes were therefore added to the figure whenever V_m crossed V_th.)

Figure 3.

Climbing activity in the LIF model based on the positive feedback loop illustrated in Figure 2. A, Left, State space spanned by the instantaneous FR of the LIF neuron and the g_ADP conductance averaged across interspike intervals (〈g_ADP〉). The 〈g_ADP〉 nullcline (dashed) is the curve that gives for each firing rate the level of 〈g_ADP〉 generated at that rate. The FR nullcline (black, solid) gives for each firing rate the amount of 〈g_ADP〉 that would be required to maintain exactly that rate. Wherever these curves intersect or overlap, the neuron receives exactly what it needs to maintain the corresponding firing rate. Here the FR nullcline is just slightly below the 〈g_ADP〉 nullcline from ∼10 to 75 Hz, such that the neuron over this range receives slightly more ADP current than would be needed to maintain any of these rates. Inset, Magnified area of the graph within the box, to better visualize the distance between nullclines. The gray line is the trajectory that the system takes through 〈g_ADP〉/FR space when briefly excited by afferent inputs. The small bump in the trajectory is caused by the brief stimulus. Right, Time graph corresponding to the left side. After a brief stimulation at 5 sec (Stim), the instantaneous firing rate slowly climbs over tens of seconds. B, C, Same as A for configurations in which the FR nullcline is shifted further downward (left) such that climbing activity rises faster (right). D, Climbing activity in an LIF neuron (solid traces) coupled to a response neuron (dashed traces) from which it receives feedback inhibition. Traces for two different synaptic input weights producing very slow or faster climbing activity are shown. Note that the system was adjusted to maintain a basal firing rate at ∼10–20 Hz, as observed in thalamus (Komura et al., 2001) and some prefrontal cortex neurons (Quintana and Fuster, 1999; Rainer et al., 1999), from which climbing activity smoothly emerges at the time of cue presentation. The slight parallel dislocation of the nullclines such that the line attractor vanishes and the system starts climbing was achieved in this case by injecting a small depolarizing current (or by stimulating excitatory external synapses) with trial onset. In a working memory or prediction task, such a stimulation might originate from neurons with plateau-like delay activity that are turned on by the cue stimulus (Fuster, 1973, 2000; Funahashi et al., 1989; Durstewitz et al., 2000). E, Climbing activity is still preserved in the presence of noise from background synaptic input.

Figure 2.

Positive feedback loop generating climbing activity. Membrane depolarization (1) triggers spiking (2), which induces opening of high-voltage-activated Ca²⁺ channels (I_Ca) via dendritic back-propagating spikes (3) leading to Ca²⁺ influx. Inflowing Ca²⁺ in turn activates Ca²⁺-dependent cation currents (I_ADP; 4), which cause further membrane depolarization (1) and spiking. Albeit not necessary for generating climbing activity (Egorov et al., 2002), the model also included recurrent and feedforward synapses as indicated by dashed lines.

Figure 8.

Hypothetical model for using a temporal difference error (TDE) to drive adjustment of the slope of climbing activity. Climbing activity via response neurons (see Fig. 3D) inhibits a population of comparator neurons at the predicted time of occurrence T_pred. Neurons coding for the to-be-predicted stimulus event (at time T_event) in contrast excite the comparator neurons. Thus, if T_pred<T_event, comparator neurons will discharge below baseline, where as they will fire above baseline if T_event < T_pred. Only if the predicted and the actual times of occurrence coincide, the firing rate of the comparator neurons will not change, because incoming signals cancel each other.

Figure 4.

Length and return time of trajectories caused by perturbations increase as the angle between the FR and 〈g_ADP〉 nullcline decreases. A, Left, State space with FR nullcline (black, solid), 〈g_ADP〉 nullcline (dashed), and a trajectory (gray, solid) around the stable fixed point caused by 300 msec depolarizing and hyperpolarizing current pulses (for briefer current steps, the perturbation in instantaneous firing rate would also depend very much on the relative phase of the interspike interval at which the step arrives). Right, Time graph of the instantaneous firing rate corresponding to the trajectory on the left. B,C, Same as A for decreasing angles between nullclines. The closer the system is to a line attractor configuration, the farther perturbations take the system away from the fixed point (left), and the slower the decay back to the steady state firing rate (right).

Figure 5.

Variance in output firing rate and [Ca²⁺]_i increases as the angle between the FR and 〈g_ADP〉 nullclines decreases. A, Variation of angles between the 〈g_ADP〉 nullcline (dashed) and the FR nullcline (solid). Three representative 〈g_ADP〉 nullclines are shown for whichγ_ADP = 1 (single stable fixed point), 4 (line attractor), and 10 (bistable neuron). B, Stable firing rates of model neurons in the presence of synaptic noise for a range of different g_ADP slopes including the cases illustrated in A. Beyond the line attractor configuration (γ_ADP > 4), neurons exhibit two different stable firing modes corresponding to the top and bottom intersections of the nullclines as for γ_ADP = 10 in A. The gap in the top curve results from the fact that for g_ADP slopes only slightly larger than that of the line attractor configuration, the top fixed points are not stable in the presence of noise (because their basins of attraction might be too small and flat). C, Firing rate as a function of time for the three representative configurations shown in A, labeled by their g_ADP slopes (γ_ADP). For the largest g_ADP slope (10), activity is shown for the system being either in its higher or lower stable activity mode (see B). Note that activity for the line attractor configuration (γ_ADP = 4) is clearly distinguished by its high variance and more prominent slow frequency components. D, Variance in firing rates (σ_FR²; black) and in intracellular Ca²⁺ concentration (σ_Ca²; gray) as a function of the slope of the 〈g_ADP〉 nullcline (γ_ADP). Both signals increase sharply as γ_ADP approaches the line attractor configuration.

Figure 6.

Variance in firing rates for neurons with the same average rate is maximal if these are in a line attractor configuration. A, State space with FR (gray, solid) and 〈g_ADP〉 (dashed) nullclines, illustrating a representative subset of the different configurations used for simulations. The 〈g_ADP〉 nullcline for the configuration closest to a line attractor almost completely covers the (gray) FR nullcline. B, Firing rate as a function of time for a neuron in the line attractor configuration (gray) compared with a neuron with randomly selected g_ADP parameters and a firing rate variance somewhere within the range shown in D (black). C, Variance in firing rates for 20 randomly selected configurations (see Results), averaged over 12 simulations with different random seeds (error bars indicate SD). Configuration 1 with the highest variance is the line attractor configuration. Note that for the line attractor configuration, also the variance of the variance of the firing rates becomes largest. D, Correlation between the magnitude of the variance in firing rates and the average distance of the 〈g_ADP〉 and FR nullclines in state space for 39 randomly selected configurations (excluding the line attractor). The smaller the average distance between nullclines, the larger the variance in firing rates. Euclidian distance was measured at different, equally spaced points within a ±10 Hz range around the fixed point and averaged across these points.

Figure 7.

Self-organization into a line attractor configuration by using the variance in internal Ca²⁺ or g_ADP as a signal (using the same parameters as in Fig. 5). A, The slope of the g_ADP nullcline (γ_ADP) quickly rotates toward the optimal region within a few sampling periods, starting from different initial conditions, although its fine adjustment might take more time. σ_gADP² was used as learning signal (for y_Ca as a signal, learning usually takes longer; for details, see Appendix, Learning algorithm). B, Rotation process of the 〈g_ADP〉 nullcline (dotted lines) toward its final position (dashed line) in state space with the FR nullcline (solid line), starting fromγ_ADP = 10. C, Same as B but starting fromγ_ADP = 1. D, Final slope of the 〈g_ADP〉 nullcline relative to the optimal slope (dashed line) averaged over 10 simulations with different random seeds, starting with a very small initial slope (γ_ADP = 1), with a slope close to the line attractor (γ_ADP = 4), or with a very high initial slope (γ_ADP = 10) and using eitherσ_gADP² or y_CA as the learning signal. Error bars indicate SD.